Most Recent Posts

10 Tips for Passing the Level I Chartered Financial Analyst (CFA) Exam

Today, we bring to you a guest post by Andrew Jones from Fitch Learning about very important tips that you need to be aware of while preparing

December Level I Results are OUT! Congratulations to 43% who passed and Short Post-Results Survey

The CFA institute has started emailing December 2013 CFA level I candidates with their exam results. The institute has announced the pass rate to be

Level III 2013 Essay Exam Now Available

Overview of December (Quarter Performance): CFA Level I Exam and Daily CFA Trivia

Overview of November Posts: Texas Plus, Cost of Capital, and Common Exam Mistakes – The Last Post for the Year

12,000 views – This is where we stand today after five months of CFA fun. I am beyond happy with all the positive feedback and

The material in this blog post is useful to the candidates preparing for: Level II of CFA Exams

Earlier this week, I have introduced the first model for option pricing which assumed discrete time movement, the binomial model. If we keep reducing the time interval between periods, then in the limits, the binomial model moves discrete time to continuous time and we move to another model called the Black-Scholes model.

• Note: Before I start this topic, Black-Scholes happens to be one of my favorite topics in finance and therefore, this reading (as well as the next two blog posts – which I’m going to talk about at the end of this post) will be quite detailed. If you are not interested in getting this type of extensive knowledge, you might want to skip this material and not use it. However, I promise that if you invest some of your time in here, you will find the knowledge you receive to be valuable.

What are the assumptions of the Black-Scholes?

Let’s first start by discussing the assumptions of Black-Scholes-Merton (hereafter, BS) model:

1. The underling price follows a lognormal probability distribution as it evolves through time – lognormal distribution is one on which the log return (asset prices) is normally distributed.
2. The risk-free rate is known and constant (continuously compounded)
3. The volatility (standard deviation of log return) is known and constant
4. There are no taxes and transaction costs
5. There are no cash flows on underlying (i.e. non-dividend-paying stock) – this assumption can be easily modified
6. The options are European – for pricing American options, the best approach is binomial model with large number of time periods.

Before we introduce BS Formula…

Remember form normal distribution that the CDF (cumulative probability function) is:

The BS Formula:

Using BS, the value for a call option is:

σ is the annualized standard deviation of the continuously compounded return on the stock

r c is the continuously compounded rate of return on a stock

• Note: From now on, anytime ‘r’ appears in Black-Scholes related formulae, then you should assume by default that we are referring to r c because returns are always continuously compounded in Black-Scholes world.

Using Put-Call Parity. the value for a put option under Black-Scholes is:

• Note: It appears that candidates are no longer required to COMPUTE the value of call or put options using Black-Scholes; however, understanding the formula is important and interpretation of the terms is important too.

What if we want to find the value at different time than 0?

If we want to measure the value of a call option in future date, then the original formula can be easily modified; using BS, the value for a call/put option is:

We use risk-neutral valuation in BS. This property is that the equation doesn’t involve any variables that are affected by the risk preferences of investors. The variables that do appear in the equation are the current stock price, time, stock price volatility, and the risk-free rate of interest. All are independent of stock preferences. The BS would not be independent of risk preferences if it involved the expected return, μ. on the stock. This is because the value of μ does depend on risk preferences.

Interpretations of Terms that appear in BS:

To provide interpretation of terms that appear in BS we note that it can be written as:

• The expression N(d₂ ) is the probability that the option will be exercised in a risk-neutral world.
• The expression S₀ e -rT N(d₁ ) is the expected value in risk-neutral world of a variable that is equal to S_T if S_T > X or 0 otherwise.

Does BS provide reasonable prices?

One way to test if the prices that the model provides are reasonable is to see if they fall within the pricing bounds. In an earlier reading, I have shown how to establish pricing boundaries on options. If we assume continuous pricing, then the pricing bounds are:

Given the following set of data:

X = 40, r c =5%, T = 2, σ = 30%

And using the Excel file that will be shown in this post later, we can show the BS price and pricing bounds on one chart for different ranges of spot prices for both a put and call options:

Does BS Make Sense?

One way to confirm if BS makes sense is to examine what happens to the option price as we change some parameters. Below, we examine three questions under BS model:

1. What happens for option price when the stock price becomes very large?
2. What happens for option price when volatility decreases (i.e. approaches zero)?
3. What happens for option price as we approach expiration?

From what we know about options, we can answer these answers theoretically and then confirm if the results under BS match our expectations.

What happens for option price when the stock price becomes very large?

Call prices increase if the stock price increases; this result is intuitive because call options are more valuable when stock prices are higher. Put prices decrease if the stock price increases; this result is again intuitive because put options are less valuable when stock prices are higher.

What happens for option price when volatility decreases (i.e. approaches zero)?

Since the investor is insured against downside movements, increase in volatility has the effect of increasing upside extremes but never affect downside extremes. Thus, the value of the option is always higher the higher the volatility. If volatility deceases, option prices should decrease to lower pricing bound.

What happens for option price as we approach expiration?

As we approach expiration, the option price should reflect more the intrinsic value than time value. At expiration, option price should reflect exactly the intrinsic value of the option. Let’s now see the answers to these questions in BS:

Case 1: What happens when stock price becomes very large?

When the price is very large, the call is almost certainly exercised and we expect the call price to be:

In BS, ceteris paribus, when S₀ becomes very large, d₁ and d₂ becomes very large leading to N(d₁ ) and N(d₂ ) to be equal to 1 and the equation for call option simplifies to the one above.

When the stock price is very large, we expect the put option to be worthless. In BS, ceteris paribus, when S₀ becomes very large, d₁ and d₂ becomes very large leading to N(-d₁ ) and N(-d₂ ) to be equal to 0 and the equation for put option simplifies to zero.

Case 2: What happens when volatility approaches zero?

Because the stock price is virtually riskless, it will grow at a rate of e rT and the payoff from the call option at maturity will be max(S₀ e rT – X, 0).  Discounting it to the present will give us e -rT [max(S₀ e rT – X, 0)]  which means the call price is max(S₀ – X e -rT. 0). To show consistency with BS, we consider 2 cases:

1. If S₀ > X e -rT , when σ is 0 then d₁ and d₂ approaches positive infinity leading N(d₁ ) and N(d₂ ) to be equal to 1 and the equation becomes S₀ – X e -rT . This is logical because if you don’t expect volatility in stock prices and the current stock price is greater than the discounted strike price then that option must sell for the intrinsic value to eliminate any arbitrage.
2. If S₀ < X e -rT , when σ is 0 then d₁ and d₂ approaches negative infinity leading N(d₁ ) and N(d₂ ) to be equal to 0 and the equation becomes equal to zero and the call is worthless. This is logical because if you don’t expect volatility in stock prices and the current stock price is less than the strike price then that option is out-of-the-money.

Case 3: What happens when option approaches expiration (t=T)?

To answer this, we need to remember first that at any time in the future (other than t = 0):

1. If S_T > X. then d₁ and d₂  approaches positive infinity (i.e. notice that the square root of time difference will approach zero and ln(S_T /X) will be positive because the ratio of S_T /X will be greater than 1)  leading N(d₁ ) and N(d₂ ) to be equal to 1 and the equation becomes S_T – X
2. If S_T < X. then d₁ and d₂   approaches negative infinity (i.e. notice that the square root of time difference will approach zero and ln(S_T /X) will be negative because the ratio of S_T /X will be less than 1)  leading N(d₁ ) and N(d₂ ) to be equal to 0 and the call expires out-of-the-money

EXCEL FILE

This file can be used to solve problems related to continuous option pricing and mainly the Black Scholes Model. Given input data, the worksheet in this file determines the price of European call or put options on securities. The file also shows how the price falls within the lower and upper pricing bounds on charts. Finally, the file shows summary of how sensitive is the option price to changes in pricing parameters (i.e. the Greeks)

The Greeks:

Greek letters are defined as the sensitivities of the option price to a single-unit change in the value of either a state variable or a parameter (i.e. stock price, volatility, risk-free rate, time to expiration …etc).Such sensitivities can represent the different dimensions to the risk in an option. Financial institutions who sell option to their clients can manage their risk by Greek letters analysis.

Delta (Sensitivity to the underlying price)

Delta can be obtained approximately from BS formula as the value of N(d₁ )  for calls and -N(-d₁ ) for puts. More formally, delta is found as (change in option price)/ (change in underlying price). I will show the derivative (which is not required for the exam) in another reading. Delta, thus, defines the sensitivity of the option price to a change in the price of the underlying.

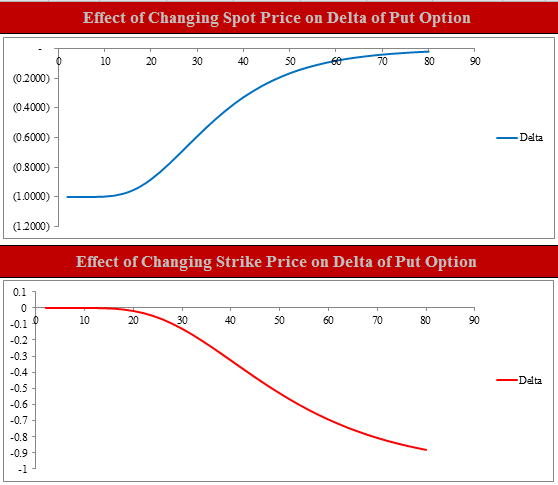
For a call, delta will increase toward 1 as the underlying price moves up and will decrease toward 0 as the underling price moves down. This makes sense because if the underlying price increases, the option is more likely to expire in the money and therefore a call buyer will buy the stock. In order to hedge the position, a short position in the stock is required. The more likely the option to expire in the money, the higher the delta; using the Excel file that will be shown in the post later, the graphs below show how delta for a call option changes for different strike and spot prices. Given the following set of data: X;S = 40, r c =5%, T = 2, σ = 30%

For a put, delta will decrease toward -1 as the underlying price moves down and will increase toward 0 as the underling price moves up. This makes sense because if the underlying price decreases, the option is more likely to expire in the money and therefore a put buyer will deliver the stock. In order to hedge the position, a long position in the stock is required. The more likely the option to expire in the money, the higher the delta (in absolute terms); using the Excel file that will be shown in the post later, the graphs below show how delta for a put option changes for different strike and spot prices. Given the following set of data: X;S = 40, r c =5%, T = 2, σ = 30%

Delta is useful in hedging. The idea is to make sure that the gain (loss) on the stock position would then tend to offset the loss (gain) on the option position. A position with Delta of zero is referred to as Delta-neutral. It is important to realize that, since the Delta of an option doesn’t remain constant, the trader’s position remains Delta hedged (or Delta neutral) for only a relatively short period of time. The hedge has to be adjusted periodically. This is known as rebalancing. A procedure where the hedge is adjusted on a regular basis is referred to as dynamic hedging. Below is a summary of the formula for delta:

In a hedging portfolio:

• For Calls: Number of hedging shares = numbers of call * N(d₁ )
• For Puts: Number of hedging shares = numbers of put* -N(-d₁ )

Gamma (Sensitivity to the underlying price sensitivity)

In general, the larger the move in the underlying, the worse the approximation of delta and the less effective it is. Just like how bond’s duration can be modified by convexity, the second-order effect in options is referred to as gamma. Gamma is a numerical measure of how sensitive the delta is to a change in the underlying. In other words, it measures how much the delta changes. When gamma is large, the delta changes rapidly and can’t provide good approximation of how much the option moves for each unit of movement in the underlying. Gamma is larger when there is more uncertainty about whether the option is going to expire in- or out-of-the-money. This means that gamma will tend to be large when the option is at-the-money and close to expiration.

It is quite risky to keep Delta-neutral portfolio unchanged for some time. As seen in the next graph, when price of underlying asset jumps to the new price, the value of the call option under the delta will underestimate the actual increase; the hedging error in this case will be C_new C_delta

The size of the hedging error depends on the curvature of the relationship between the option price and the stock price. Gamma measures this curvature. Gamma is calculated using the following formula (nor the formula or its derivation which I am going to provide in another reading are required for the exam – what matters is knowing that Gamma for calls and puts are the same and it is highest when option is at the money)

Using the Excel file that will be shown in the post later, the graphs below show how Gamma for an option (call and put are the same) changes for different strike and spot prices. Given the following set of data: X;S = 40, r c =5%, T = 2, σ = 30%

Gamma hedging: A position in the underlying asset has zero Gamma and can’t be used to change the Gamma of a portfolio. What is required is a position in an instrument such as an option that is not linearly dependent on the underlying asset. Making a portfolio Gamma-neutral as well as Delta-neutral can be regarded as correction for the hedging error. Delta neutrality provides protection against relatively small stock price moves between rebalancing. Gamma neutrality provides protection against larger movements in this stock price between rebalancing.

Theta (Sensitivity to the time to expiration)

For European options, all of the price can be viewed as time value. Time value is a function of the option’s moneyness, the option’s time to expiration, and its volatility. As expiration approaches, the option price moves toward the payoff value of the option at expiration, a process known as time value decay. The rate at which the time value decays is called the option’s theta. Both call and put values decrease as the time to expiration decreases. Most of the time, option prices are higher the longer the time to expiration. For European options, however, some exceptions exist. Theta is calculated using the following formula (nor the formula or its derivation which I am going to provide in another reading are required for the exam)

Theta of a call is generally negative (i.e. both terms are negative). The value of a call option goes down as time elapses both because the variance of the final price goes down and because the exercise price is less heavily discounted. The fact that theta for a call is negative doesn’t imply that call price is expected to fall; this is because the stock price is expected to rise over time: time is not the only thing that changes over time.

The variation of Theta with stock price for a call option on stock should be considered. When the stock price is very low (i.e. option is out of the money), Theta of a stock is very low (i.e. zero). For at the money options, Theta is large and negative. As price becomes larger, d₁ and d₂ approaches 1, N ’ (d₁ ) gets close to zero and N(d₂ ) gets close to one and Theta tends to become  –rXe -rT. Using the Excel file that will be shown in the post later, the graphs below show how Theta for call and put options changes for different strike and spot prices. Given the following set of data: X;S = 40, r c =5%, T = 2, σ = 30%

Keep in mind that the Theta obtained is annualized. In order to obtain daily Theta, we can divide by 365 days to obtain Theta per calendar day or by 252 to obtain Theta per trading day.

Theta is not used in hedging. While it makes sense to hedge against changes in the price of the underlying asset, it doesn’t make any sense to hedge against passage of time. In spite of this, many traders regard Theta as useful figure because it is a proxy for Gamma.

Vega (Sensitivity to volatility)

The relationship between the option price and volatility is called Vega. We should know that Vega is positive for both calls and puts and means that if volatility increases, both call and put prices increase (we explained why before). Vega is calculated using the following formula (nor the formula or its derivation which I am going to provide in another reading are required for the exam)

Vega is the same for calls and puts. It’s always positive and close to 0 when the option is either deep in-the-money or deep out-of-the-money; it is highest when spot price is closest to discounted value of strike price.

Using the Excel file that will be shown in the post later, the graphs below show how Vega for an option (call and put are the same) changes for different strike and spot prices. Given the following set of data: X;S = 40, r c =5%, T = 2, σ = 30%

Rho (Sensitivity to risk-free rate)

The sensitivity of the option price to the risk-free rate is called the rho. Technically, the BS assumes constant risk-free rate so it meaningless to talk about changing rate over life of option. There is little change occurs in the option over a very broad range of the risk-free rate. Indeed, the price of a European option on an asset is not very sensitive to the risk-free rate. Rho is calculated using the following formula (nor the formula or its derivation which I am going to provide in another reading are required for the exam)

EXCEL FILE

This file can be used to solve problems related to continuous option pricing and mainly the Black Scholes Model. Even though you are not required to calculate the Greeks for Level II, this file would show the impacts of changing strike prices and spot prices on the main Greeks: Delta, Gamma, Theta, Vega, and Rho.

The Effect of CF on the Underlying

If there are CF on the underlying, we simply use S₀ – PV(CF,0,T) in the BS model instead of S₀. If we use continuously compounded dividend rate then we discount by the dividend yield for the S₀ input in the BS formula.

1. Historical volatility: the most logical starting place to look for an estimate of future volatility is past volatility.
2. Implied volatility: in a market in which options are traded actively, we can reasonably assume that the market price is an accurate reflection of its true value. The procedure enables us to determine the volatility that option traders are using to price the option. The volatility is called the implied volatility. Unfortunately, circularity exists in the argument. If one uses BSM model to determine if an option is over- or underpriced, the procedure for extracting the implied volatility assumes that the market correctly prices the option.

• Note: In the next two blog posts, I will show for those interested how to derive Black-Scholes formula and how to derive the Greeks. None of this material appears in the CFA curriculum and it is NOT required for the exam. This is simply for those interested in learning more.

For Typos/Questions: