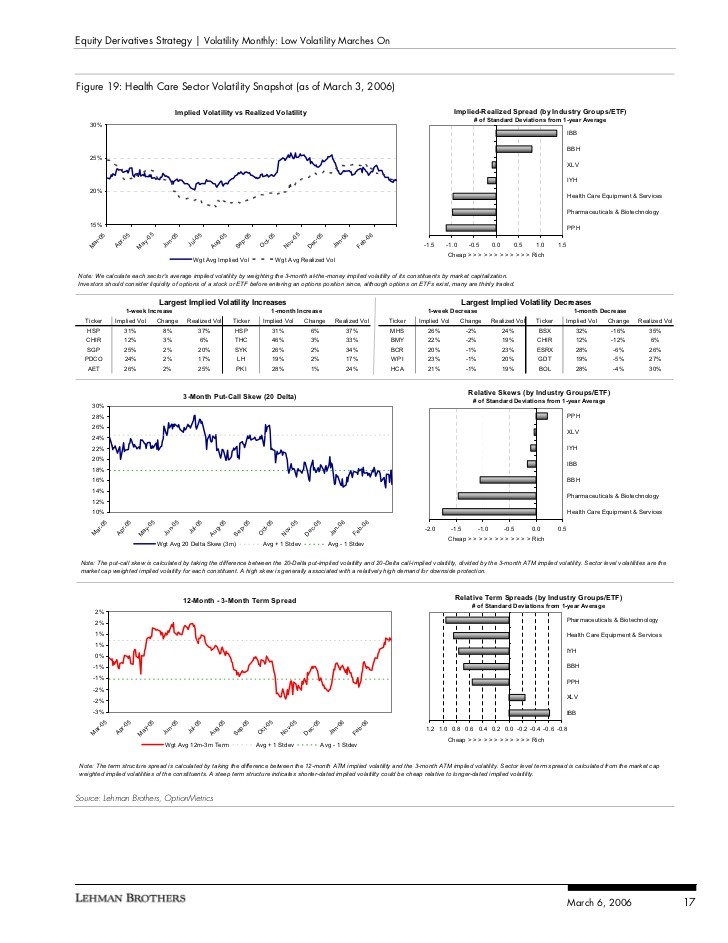
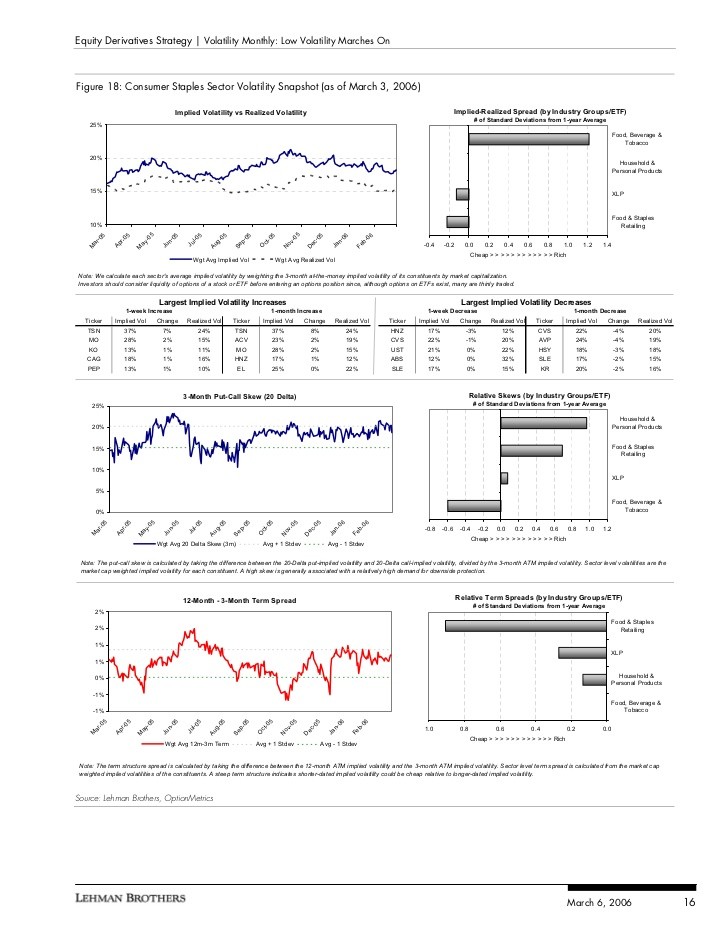
What Does Implied Volatility Skew Measure
Post on: 16 Март, 2015 No Comment
Page 1
What Does Implied Volatility Skew Measure?
Scott Mixon∗
May 2010
Abstract
This paper provides theoretical guidance and empirical analysis aimed at differentiating
among implied volatility skew measures. Industry analysts and academics use a variety of
measures, but most have little formal justification. I find that most commonly used skew
measures are difficult to interpret without controlling for the levels of both volatility and
kurtosis. Many ad hoc measures fail to meet the conditions for a valid skewness ordering. My
preferred measure is the (25 delta put volatility — 25 delta call volatility) / 50 delta volatility;
among the measures considered, it is the most descriptive and least redundant.
keywords: options, implied volatility skew
∗Lyxor Asset Management Inc. 1251 Avenue of the Americas, New York, NY 10020, (203) 561-6676
(otismixon@hotmail.com).
This paper reflects the opinions of the author and does not reflect the opinions of
Lyxor Asset Management Inc. I thank Bill Bane, Nikunj Kapadia, and Dan Kryzman for helpful comments on
earlier drafts.
Page 2
What Does Implied Volatility Skew Measure?
This paper provides theoretical guidance and empirical analysis aimed at differentiating among
implied volatility skew measures. Industry analysts and academics use a variety of measures, but
most have little formal justification. I find that most commonly used skew measures are difficult to
interpret without controlling for the levels of both volatility and kurtosis. Many ad hoc measures
fail to meet the conditions for a valid skewness ordering. My preferred measure is the (25 delta put
volatility — 25 delta call volatility) / 50 delta volatility; among the measures considered, it is the
most descriptive and least redundant.
Page 3
What Does Implied Volatility Skew Measure?
1Introduction
Equity derivatives traders and analysts monitor the implied volatility skew each day, yet there is
little practical advice to guide them. What is the best measure of the skew? How should one
compare skew for a 25% volatility stock with skew for a 50% volatility stock? Is there any intuition
suggesting what “large”, “small”, or “too much” skew would be? What does the implied vol skew
mean, anyway? This paper provides theoretical guidance, backed by empirical analysis on S&P 500
and single stock options, on these issues.
Exhibit 1 illustrates the practical difficulties facing the derivatives researcher. The chart shows
two plausible measures of skew for three month S&P 500 options, each used by Wall Street strate-
gists. The heavy line shows the 25-delta put volatility minus the 25-delta call volatility. The thin
line shows this variable normalized by the 50-delta implied volatility. The series are both stable
in 2005 and show a slightly increased skew in 2006. The divergence begins around May 2007, as
the normalized series begins suggesting a skew that declines during the next two years, in contrast
to the increasing skew of the other measure. At the end of 2009, the normalized measure indi-
cated that the skew was at average levels, whereas the non-normalized version shows a skew that
is very steep and well above average (“rich”). A researcher comparing implied volatility for 10%
out-of-the-money puts and 10% out-of-the-money calls would also find highly conflicting signals
from non-normalized and normalized versions of his series. Both skew measures seem plausible, but
which (if either) was telling the truth?
The finance literature has not provided a clear lead in defining a best practice version of skew.
This paper fills the gap with a rigorous examination of common, ad hoc skew measures. To prevent
confusion, it is worth elaborating on the technical terms used in this paper. I always use the terms
“skew” or “implied volatility skew” as a measure of the slope of the implied volatility curve for
a given expiration date, while “skewness” means the skewness of an option implied, risk neutral
probability distribution.
Page 4
A variety of skew measures, most with little theoretical motivation other than plausibility, have
been used in previous studies. Some of the methodologies are summarized in Exhibit 2. Researchers
have used regression-based values (Bakshi, Kapadia and Madan [2003]), arithmetic differences in
out-of-the-money (OTM) put volatility and OTM call volatility (defined in percentage moneyness)
(Bates [1991]), arithmetic differences of put and call volatilities based on delta (Hull, Nelken, and
White [2004]), and normalized versions of these last two variables (Toft and Prucyk [1997], Carr
and Wu [2007], and Mixon [2009]), among others.
A number of researchers, such as Dennis and Mayhew [2001], have moved toward analyzing a
model-free version of the underlying distributional skewness (standardized third central moment)
implicit in option prices. The relevant issues are not 100% settled yet: Dennis and Mayhew, for
example, reverse the conclusions of Toft and Prucyk by using a different measure of skew. Xing,
Zhang, and Zhao [2010] find that future stock returns are predictable based on the implied volatility
skew, but returns are not predictable based on option-implied skewness.
Previous researchers have used series expansions and linear approximations to derive analytical
expressions relating implied volatility to characteristics of the underlying’s distribution. Backus,
Foresi, and Wu [2004] find that their approximations work best for options on underlyings with a
modestly skewed distribution. Carr and Wu [2005] extend the analysis and approximate skewness
as proportional to the difference between volatilities for a call and a put equally out of the money
in delta terms (i.e. a risk reversal), divided by the at-the-money implied volatility.
Bakshi, Kapadia, and Madan (henceforth, BKM) [2003] also connect risk neutral moments
and the implied volatility skew; their empirical tests provide substantial support for their theory.
This paper builds on BKM’s research to provide further intuition on the structure of the skew
and its connections with some standard practitioner rules of thumb for measuring the skew. The
analysis provides practical suggestions on choosing from and interpreting some common ad hoc
skew measures.
The contributions of this paper are as follows. First, I provide a theoretical examination to
determine whether several commonly used measures of the implied volatility skew define a valid
Page 5
skewness ordering as defined in the statistics literature. Second, I use regression analysis to test
the theory against both index and single stock option data. I empirically decompose these ad hoc
measures into the portions attributable to the volatility, skewness, and kurtosis of the underlying
risk-neutral distribution implicit in option prices. The decomposition provides insight into the
characteristics each skew measure is actually capturing.
As a by-product of the analysis, I provide economic intuition about interpreting risk-neutral
moments derived from option prices. For example, BKM reported that the average level of skewness
implicit in S&P 100 options from 1991-1995 was -1.09, while the average skewness for single stocks
over that period was much closer to zero (averaging -0.31 for the 30 stocks they examined). How
does one interpret those numbers in terms of economically meaningful constructs? This paper
provides clear direction on that issue.
I find the following results. Ceteris paribus, the ad hoc skew measures move in the appropriate
direction when there is a change in the skewness for the distribution of the underlying asset, but the
relation is generally quite dependent on the level of ATM volatility. Such measures do not appear
to satisfy a key property to be a valid measure of skewness (location and scale invariance). In
practical terms, analysis of a time series of an ad hoc implied volatility skew may provide few clues
to the absolute level of skewness or its economic importance. At best, week to week changes in the
volatility skew might be a reasonable proxy for changes in skewness; similarly, movements in the
level of skew over short intervals might be an acceptable proxy when other factors (e.g. volatility
and kurtosis) are roughly constant. It is clear, however, that these measures should be treated with
caution and represent the amalgamation of several factors.
The dependence of the ad hoc skew measures on the level of ATM volatility also means that
regressions incorporating these measures as a proxy for skewness are likely misspecified. If a de-
pendent variable is regressed on, say, 90% strike volatility minus 110% strike volatility instead of
skewness, the regression omits the interaction term to control for this dependence. Including the
level of volatility on the right hand side is not a sufficient control, as the omitted variable is a
product of volatility and skewness. The resulting bias is likely to render statistical inference on














