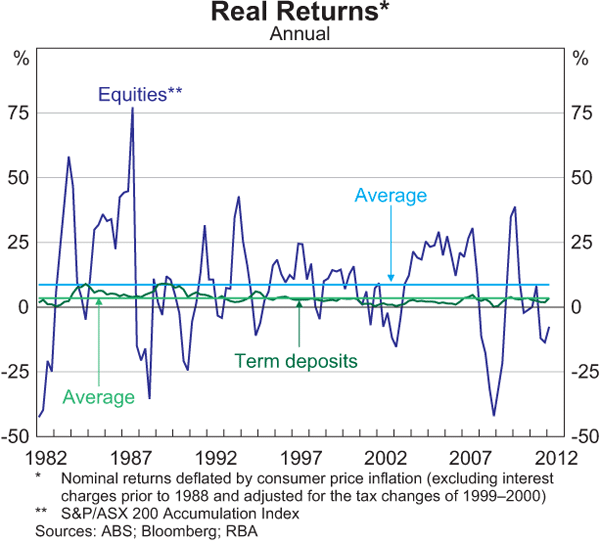
In theory, stocks should provide a greater return than safe investments like Treasury bonds. The difference is called the equity risk premium. it is the excess return that you can expect from the overall market above a risk-free return. There is vigorous debate among experts about the method employed to calculate the equity premium and, of course, the resulting answer. In this article, we take a look at these methods — particularly the popular supply-side model — and the debates surrounding equity premium estimates.

Why Does It Matter?

The equity premium helps to set portfolio return expectations and determine asset allocation policy. A higher premium, for instance, implies that you would invest a greater share of your portfolio into stocks. Also, the capital asset pricing relates a stock’s expected return to the equity premium: a stock that is riskier than the market — as measured by its beta — should offer excess return above the equity premium.

Greater Expectations

Compared to bonds, we expect extra return from stocks due to the following risks:

1. Dividends can fluctuate, unlike predictable bond coupon payments.
2. When it comes to corporate earnings, bond holders have a prior claim while common stock holders have a residual claim.
3. Stock returns tend to be more volatile (although this is less true the longer the holding period ).

And history validates theory. If you are willing to consider holding periods of at least 10 or 15 years, U.S. stocks have outperformed treasuries over any such interval in the last 200 years.

But history is one thing, and what we really want to know is tomorrow’s equity premium. Specifically, how much extra above a safe investment should we expect for the stock market going forward? Academic studies tend to arrive at lower equity risk premium estimations — in the neighborhood of 2-3%, or even lower! Later in this article, we’ll explain why this is always the conclusion of an academic study, whereas money managers often point to recent history and arrive at higher estimations of premiums.

Getting at the Premium

Here are the four ways to estimate the future equity risk premium:

What a range of outcomes! Opinion surveys naturally produce optimistic estimates, as do extrapolations of recent market returns. But extrapolation is a dangerous business: first, it depends on the time horizon selected, and second, we cannot know that history will repeat itself. Professor William Goetzmann of Yale has cautioned, History, after all, is a series of accidents; the existence of the time series since 1926 might itself be an accident. For example, one widely accepted historical accident concerns the abnormally low long-term returns to bondholders that started right after World War II (and subsequently low bond returns increased the observed equity premium); bond returns were low in part because bond buyers in the 1940s and 1950s — misunderstanding government monetary policy — clearly did not anticipate inflation .

Building a Supply Side Model

Let’s review the most popular approach, which is to build a supply-side model. There are three steps:

1. Estimate the expected total return on stocks.
2. Estimate the expected risk-free return (bond).
3. Find the difference: expected return on stocks minus risk-free return equals the equity risk premium.

We’ll keep it simple and sidestep a few technical issues. Specifically, we are looking at expected returns that are long-term, real, compound and pre-tax. By long-term, we mean something like 10 years, as short horizons raise questions of market timing. (That is, it is understood that markets will be over or under-valued in the short run.)

By ‘real’, we mean net of inflation. Even if we estimated the stock and bond returns in nominal terms, inflation would fall out of the subtraction anyhow. And by ‘compound’, we mean to ignore the ancient question of whether forecasted returns ought to be calculated as arithmetic or geometric (time-weighed) averages.

Finally, although it is convenient to refer to pre-tax returns as do virtually all academic studies, individual investors should care about after-tax returns. Taxes make a difference. Let’s say the risk-free rate is 3% and the expected equity premium is 4%; we therefore expect equity returns of 7%. Say we earn the risk-free rate entirely in bond coupons taxed at ordinary income tax rates of 35%, whereas equities may be deferred entirely into a capital gains rate of 15% (i.e. no dividends). The after-tax picture in this case makes equities look even better.

Step One: Estimate the Expected Total Return on Stocks

Dividend-Based Approach

The two leading supply-side approaches start with either dividends or earnings. The dividend-based approach says that returns are a function of dividends and their future growth. Consider an example with a single stock that today is priced at $100, pays a constant 3% dividend yield (dividend per share divided by stock price), but for which we also expect the dividend — in dollar terms — to grow at 5% per year.

In this example, you can see that if we grow the dividend at 5% per year and insist on a constant dividend yield, the stock price must go up 5% per year too. The key assumption is that the stock price is fixed as multiple of the dividend. If you like to think in terms of P/E ratios. it is the equivalent to assuming that 5% earnings growth and a fixed P/E multiple must push the stock price up 5% per year. At the end of five years, our 3% dividend yield naturally gives us a 3% return ($19.14 if the dividends are reinvested). And the growth in dividends has pushed the stock price to $127.63, which gives us an additional 5% return. Together, we get a total return of 8%.

That’s the idea behind the dividend-based approach: the dividend yield (%) plus the expected growth in dividends (%) equals the expected total return (%). In formulaic terms, it is just a re-working of the Gordon Growth Model. which says that the fair price of a stock (P) is a function of the dividend per share (D), growth in the dividend (g) and the required or expected rate of return (k):