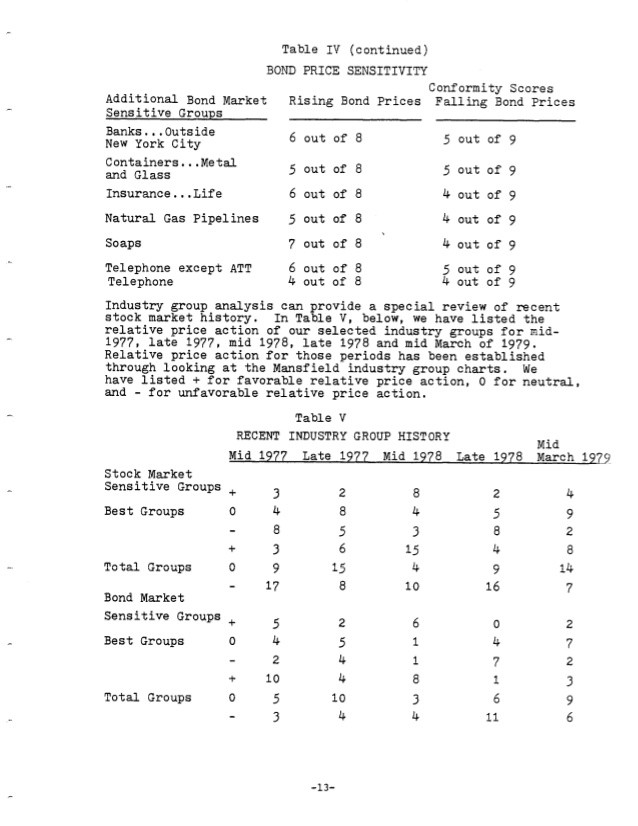
Page 1

Price Trends and Patterns in Technical Analysis:

University of Iowa

Geoff C. Friesenb

University of Nebraska-Lincoln

Lee M. Dunhamc

University of Nebraska-Lincoln

Draft Date: August 2007

JEL Classification: G14, G11, G12, C1

Keywords: Technical Analysis, Trading Rules, Equity Jumps, Momentum, Confirmation Bias

a Henry B. Tippie College of Business, Department of Finance, S252 Pappajohn Business Bldg. Iowa City, IA

52242-1994. Email: paul-weller@uiowa.edu. Tel: 319.335.1017. Fax: 319.335.3690.

b Corresponding author. Department of Finance, 237 CBA, Lincoln, NE 68588-0490. Email: gfriesen2@unl.edu.

Tel: 402.472.2334. Fax: 402.472.5140.

c Department of Finance, 233 CBA, Lincoln, NE 68588-0490. Email: ldunham2@unl.edu. Tel: 402.472.2325. Fax:

Page 2

Abstract

We develop a formal model of asset prices in which investors are subject to confirmation bias,

which describes the tendency of individuals to search for and interpret information selectively to

conform to a given set of beliefs. The model produces three notable results. First, the model

generates price patterns which validate certain well-documented trading strategies, in particular

the “head-and-shoulders” pattern. Second, asset prices exhibit negative autocorrelations over

very short horizons, positive autocorrelations over intermediate horizons, and negative

autocorrelations over long horizons, which matches the observed stylized properties of U.S.

equity prices. Third, the model predicts that sequential price jumps for a particular stock will be

positively autocorrelated. Several recent econometric papers have shown that one can identify

significant jumps by comparing realized volatility and bi-power return variation. Using this

methodology, together with tick-by-tick data on all stocks in the S&P 100 index from 1999-

2005, we identify and calculate significant jumps in stock prices. Consistent with the predictions

of the model, we find that jumps exhibit statistically and economically significant positive

autocorrelations.

Page 3

1. Introduction

Technical analysts use information about historical movements in price and trading

volume, summarized in the form of charts, to forecast future price trends in a variety of financial

markets. The claims of technical analysts were initially discounted by the academic community

on the grounds that they were inconsistent with market efficiency. But recent work has called

into question the extent to which markets are fully efficient. There is now convincing evidence

that stock prices display short-term momentum over periods of six months to a year and longer-

term mean reversion (De Bondt and Thaler, 1985; Chopra, Lakonishok and Ritter, 1992;

Jegadeesh and Titman, 1993). This provides support for a particular class of technical trading

rule that is designed to detect persistent trends. Such rules have been shown to perform profitably

in foreign exchange markets (Dooley and Shafer, 1983; Sweeney, 1986; Levich and Thomas,

1993; Neely, Weller and Dittmar, 1997). There is also evidence of economically significant price

reversals over short time horizons of a week to a month (Jegadeesh, 1990; Jegadeesh and

Titman, 1995; Lehmann, 1990; Gutierrez and Kelley, 2007).1

Various theoretical arguments have been advanced to explain the observed patterns of

momentum and reversal (see e.g. Barberis, Shleifer and Vishny, 1998; Daniel, Hirshleifer and

Subrahmanyam, 1998, Hong and Stein, 1999). These models introduce various departures from

fully rational behavior, and imply that investors using trading rules of the trend-following variety

may be able to profit from these departures from rationality.

The use of technical signals based on price patterns has received less academic attention,

despite the fact that these signals are widely used by practitioners. Chang and Osler (1999)

examine the profitability of using the “head-and-shoulders” pattern in the foreign exchange

1 Conrad, Kaul and Nimalendran (1991) demonstrate that bid-ask bounce explains some of this return reversal.

Cooper (1999) and Subrahmanyam (2005) find that microstructure issues cannot fully explain the documented

return reversal.

Page 4

market to predict changes of trend, and find evidence of excess returns for some currencies but

not others. Lo, Mamaysky and Wang (2000) develop a pattern detection algorithm based on

kernel regression. They apply this methodology to identify a variety of technical price patterns

including “head-and-shoulders” in the U.S. stock market over the period 1962 — 1996. They find

statistical evidence that there is potentially useful information contained in most of the patterns

they consider. Savin, Weller and Zvingelis (2007) show that a modified version of the algorithm

of Lo, Mamaysky and Wang applied to the “head-and-shoulders” pattern has substantial

predictive power for U.S. stock returns over periods of one to three months.

The aim of this paper is to develop a theoretical framework that can account for the

apparent success of both trend-following and pattern-based technical trading rules. We introduce

a single cognitive bias into the model, that of confirmation bias. The bias is a phenomenon that

has been extensively documented in experimental studies. It refers to the search for, or the

interpretation of evidence in ways that favor existing beliefs or expectations. It has been

described as “perhaps the best known and most widely accepted notion of inferential error to

come out of the literature on human reasoning.” (Evans, 1989, p.41 quoted in Nickerson, 1998).

A related phenomenon has been extensively investigated in the management literature

under the heading of “escalation of commitment.” This research seeks to provide explanations

for commitment within organizations to losing courses of action. Theoretical explanations often

focus on the theory of cognitive dissonance (Festinger, 1957). It is argued that people who are

responsible for poor decisions seek to rationalize them by biasing their interpretation of

information relevant for assessing the outcome of the decisions. A study of the banking industry

found that bank executive turnover predicted both provisions for loan losses and the write-off of

bad loans (Staw, Barsade and Koput, 1997). The implication of these findings is that those

Page 5

individuals responsible for making the original loan decisions exhibited systematic bias in their

interpretation of information about the status of the loans.

A specific example of how confirmation bias is recognized as a potential source of

inefficiency within the investment community is provided by Camerer and Loewenstein (2004,

p.17). They report how an investment banker had described the way in which his firm combated

the effects of traders’ “emotional attachment to their past trades” by periodically forcing traders

to switch positions with each other. In a study looking at dissonance effects in the context of

mutual fund investment, Goetzmann and Peles (1997) found that even well-informed investors

had a tendency to favorably distort their perceptions of the past performance of funds that they

held. This may explain the observed asymmetry between investment flows into winning funds

and out of losing funds (Ippolito, 1992).

Confirmation bias has also been shown to manifest itself in group decision making

(Schulz-Hardt, Frey, Lüthgens and Moscovici, 2000). Using a sample of middle managers from

banks and industrial companies, the experiment involved analysis of a case study in which a

company has to decide whether or not to proceed with a large investment. Subjects were required

to come to a preliminary conclusion individually before being combined into groups. At this

point they were given access to additional information. Groups that agreed in their preliminary

conclusions showed a strong preference for accessing supporting rather than conflicting

information. This finding is of particular interest in the present context, since many portfolio

investment decisions are the outcome of group deliberations.

In our model, information arrival is modeled with signals of various magnitudes, arriving

at differing frequencies. Large, infrequently observed signals are interpreted rationally by

investors. However, investors’ interpretation of less informative signals (which arrive more

Page 6

frequently) is biased by the recently observed large signals. The model generates price patterns,

most notably the “head-and-shoulders” pattern, which have the predictive power for future stock

returns claimed by technical analysts. The model thus provides a theoretical foundation for

several price patterns commonly used by technical analysts. The model also produces the well-

documented pattern of price momentum which can be exploited by trend-following technical

rules such as those based on the comparison of short- and long-run moving averages.

In addition, our model makes several predictions. First, return autocorrelations are

negative over very short horizons, positive over intermediate horizons, and become negative

again over long horizons. This feature of the model conforms to the empirical properties of U.S.

equity prices described above. Our model also produces a sharp prediction that the time series of

jumps in the price series should be positively autocorrelated. To our knowledge, this is a new

and untested empirical prediction.

We provide empirical evidence that confirms the prediction of our model that sequential

price jumps in equity prices are positively autocorrelated. Specifically, we utilize the statistical

bi-power variation estimation technique to identify all statistically significant jumps in the price

series of the individual component stocks of the S&P 100 Index over the sample period 1999-

2005. We find that sequential price jumps exhibit statistically and economically significant

positive autocorrelations, and that these autocorrelations decay at a rate that is also consistent

with the model.

Our model and empirical tests complement the recent empirical work of Gutierrez and

Kelley (2007). They document negative weekly autocorrelations immediately after extreme

information events, but find that momentum profits emerge several weeks after an extreme return

and persist over the remainder of the year. Moreover, this momentum easily offsets the brief and

Page 7

initial return reversal. Our model produces predictions consistent with this finding. They also

find that markets react similarly to explicit (public) and implicit (private) news, and note that

many behavioral models require investors to react differently to different types of news. In

contrast, our model makes no distinction between public and private news.

The rest of the paper is organized as follows: Sections 2 and 3 present the model.

Section 4 describes various trading rules and relates them to the model. In Section 5 we describe

our jump detection methodology, and in Section 6 present empirical results. Section 7

concludes.

2. The model with a single low-frequency signal

The process by which information is revealed and incorporated into prices is constructed

to capture the important features of a jump-diffusion process in a discrete-time framework. The

jump-diffusion model of stock returns has a long history (Merton, 1976) and recent work by

Barndorff-Neilsen and Shephard (2004) indicates that jumps in equity prices contribute a

significant proportion of total price volatility. Research on empirical option pricing has also

found that introducing jump components into the underlying price series alleviates some of the

pricing biases found in standard models (Bates, 2003). We suppose that there are low-frequency

signals that are more informative than high-frequency signals. One can think of the low-

frequency signals as generating the jumps in the price series, and the high-frequency signals as

generating the diffusion. There is a single representative investor who is assumed to be risk

neutral, and who observes a low-frequency signal (L-signal) at date 0 about the liquidation value

of a security. At subsequent dates, a sequence of high-frequency signals (H-signals) is observed.

At date T, all information about security value is revealed and the investor receives its liquidation

value.

2.1 Model Specification

The risky security has a liquidation value