Journal of Asset Management (2007) 8, 5872. doi:10.1057/palgrave.jam.2250060

Alpha budgeting Cross-sectional dispersion decomposed

Wallace Yu 1 and Yazid M Sharaiha 2

Correspondence: Yazid M. Sharaiha, 25 Cabot Square, London E14 4QA, UK. E-mail: yazid.sharaiha@morganstanley.com

1 is Vice President in Global Markets Equity at Deutsche Bank AG London. He holds a Master’s in Mathematical Finance from Imperial College, London (2001) and is a CFA charterholder. This paper was co-authored when he was at Morgan Stanley’s Quantitative and Derivative Strategies group.

2 is Managing Director at Morgan Stanley where he heads the Quantitative and Derivative Strategies group. He holds a Master’s in Engineering from UC Berkeley and a PhD in Operations Research from Imperial College, London (1991). He has co-authored one book and published over 30 articles in the fields of optimisation and financial modelling.

Received 1 February 2007; Revised 1 February 2007.

Abstract

(All work in this paper is based on research conducted by the two authors working for Morgan Stanley and the findings have appeared in the Morgan Stanley Quantitative and Derivative Strategies publication as of March 2006). The last three years have witnessed markedly lower volatility in global equity markets, combined with higher correlation and lower dispersion. This has meant greater challenges for asset allocation and stock selection alpha opportunities appear limited. How should the investment process be structured to maximise exploitation of the available alpha? We introduce cross-sectional standard deviation (or dispersion) as a metric for alpha opportunities, and show how it can shed light on the management of research resources, and on the optimal combination of investment strategies. The metric allows for objective alpha budgeting in the investment process. This involves both the identification of the key top-down drivers of dispersion in a given market regime, and the appropriate ‘alpha granularity’, which is linked to the optimal concentration of stocks in the portfolio. Alpha budgeting from top-down allocations country, sector, size, style and beyond: using a novel decomposition framework of cross-sectional dispersion, we show the relative magnitude of top-down allocation decisions for several organisational structures. In Europe, sector investing continues to provide greater opportunities than country investing. Alpha opportunities and volatility hedging opportunities: we establish a linkage between cross-sectional standard deviation (dispersion) and time-series correlation and volatility. Low return dispersion can be a business model risk for active stock pickers; we show how targeted exposure to volatility can be used as a hedge.

Keywords:

cross-sectional volatility, dispersion, alpha budgeting, risk decomposition, portfolio construction

Introduction

The last three years have witnessed markedly lower volatility in global equity markets, combined with higher correlation and lower dispersion. This has meant greater challenges for asset allocation and stock selection alpha opportunities appear limited. How should the investment process be structured to maximise exploitation of the available alpha?

In this paper we argue that, in addition to setting risk and return targets, understanding the current ‘alpha granularity’ in the market is critical. By this, we mean the concentration of alpha opportunities across top-down and bottom-up decisions. Cross-sectional return dispersion and its sources are important metrics for alpha granularity. Our modelling of return dispersion uncovers several attractive characteristics we show how it can be decomposed into separate top-down and bottom-up components, in line with an active investment process. Such delineation can provide guidelines for designing portfolio bet structures.

We also show the exact mathematical linkage between (cross-sectional) return dispersion and (time-series) volatility and correlation, and focus on the impact of changes in volatility and correlation on available alpha opportunities. We highlight possible hedging strategies to protect against changes in return dispersion.

Previous studies

There have been studies on the broad subject of ‘alpha granularity’ by examining return dispersion, which is closely related to the notion of diversification from a risk management perspective. Solnik and Roulet (2000) introduced a metric of cross-sectional correlation to estimate global correlation levels and trends of equity returns via a single-factor model. It is highlighted that maximising global dispersion, thus minimising global correlation, should be a major objective of global asset allocation. This aim should be an evolving target contingent on the prevailing correlation structure of global markets. To this end, a tractable measure of ‘alpha availability’ should be useful to gauge the potential success of differentiating winners from losers. Hwang and Salmon (2004) developed statistical measures to test for herding or contagious behaviours in different stock markets.

Intrinsic to the application of cross-sectional volatility in any investment process is its close relationship with time-series volatility linkages between these two volatility variables and their statistical properties were examined in great detail in Hwang and Satchell (2001) via linear factor models. There have also been attempts to incorporate the former in forecasting both market risk and market returns. See, for example, Hwang and Satchell (2005) and Goyal and Santa-Clara (2003). respectively for these two research areas.

While previous studies have largely focussed on unravelling the mathematical properties of return dispersion, which provides an extra dimension of understanding in stock co-movements within a given markets, less emphasis has been placed on how to incorporate this additional information in the area of portfolio construction. In this paper, we propose a new framework to study cross-section volatility in a portfolio context and its relation to overall market return distribution. It is our contention that establishing such a linkage is useful in channelling optimal research resources under constraints for an active asset manager in the reality world.

This paper is organised as follows: in the next section, we revisit the use of linear factor models to ascertain any herding effects in a given market. In the following section, we introduce our decomposition approach in separating ‘alpha budget’ into top-down asset allocation and bottom-up stock selection components. In the penultimate section, we establish a linkage between cross-sectional dispersion and time-series correlation and volatility using continuous-time financial mathematics. Conclusions follow in the last section.

Return dispersion and alpha opportunity

The evolution of cross-sectional return dispersion over time the distribution of asset returns is an important metric in determining both the absolute and relative attractiveness of investment strategies. Cross-sectional dispersion can be described by a number of different metrics, such as range, inter-quartile range and mean absolute deviation. Cross-sectional volatility is a particularly attractive metric for dispersion, since it considers the entire collection of returns from a sample at a given point in time. In its unweighted form, cross-sectional variance (or volatility squared) is given by:

where is the unweighted 1 market return.

Alternatively, in matrix form _t 2 =r _t T Mr _t where r _t T =(r _1t . r _2t . r _Nt ), that is, the vector of asset returns and M =1/N (I -(1 1 T / N )) with a conformable identity matrix and two conformable vectors of ones.

Throughout, we use dispersion and cross-sectional standard deviation of returns ( _t ) interchangeably.

Figure 1 shows the evolution of this cross-sectional dispersion measure for MSCI Europe and MSCI US, together with their (time-series) market volatility and cumulative (equally-weighted) market returns. On the face of it, they appear to confirm the view that the current market is characterised by low risk and low (excess) stock alpha. It appears that the market factor is at work in pinning down dispersion most of the absolute return opportunities come from market effects. This raises the question of where the remaining alpha opportunities reside, which should guide both research efforts and risk allocation decisions.

Comparison of dispersion with volatility

Full figure and legend (285K )

Herding effect Market beta compression

We can utilise our dispersion metric to investigate stock return homogeneity under varying market regimes changes in dispersion can be linked to broad market factors. This may be particularly relevant for long-only (longshort) investors with specific (net) beta targets. Low beta dispersion could lead to unintended market neutrality in portfolios. Particularly for active managers, this might mean that little incremental alpha is being generated from stock selection, with the fund only being compensated for market factor risk. Active managers may want to avoid stocks that show a ‘herding’ tendency towards the market.

Previous research such as Hwang and Salmon (2004) has studied market herding behaviours in a tractable framework. The objective of this subsection is to re-visit the problem with emphasis on empirical results.

We now use a single-index market model to study individual stock returns (assuming zero risk-free interest rate):

where r _mt is the unweighted market return defined above.

Plugging this model into our first equation, we can easily extract the beta dispersion component from total return dispersion, as follows (let _t 2 ( ) denote the dispersion operator at time t ):

Here it is assumed that systematic and idiosyncratic risks in this model are also cross-sectionally uncorrelated, and residuals terms have zero cross-sectional expectation.

Hence, under the assumption that the residuals _it are uncorrelated with the market return r _mt and to each other, it is shown that the total stock dispersion metric can be expressed as a function of beta dispersion and non-market return dispersion.

Figure 2 shows the evolution of beta dispersion for Europe and the US. Both markets show beta compression, with beta dispersion dropping from highs of around 1.4 in 2001 to lows of around 0.7 in 2003. Herding towards the market portfolio started earlier in Europe than in the US. Beta dispersion in the US has recovered somewhat since the lows in 2003, while that in Europe has continued to stay low. At the same time, overall dispersion in both markets has remained low reflecting low market volatility.

Market beta dispersion

Full figure and legend (218K )

We want to investigate any size effects despite time-varying dispersion. It is trivial to sort companies by market capitalisation, bucket them into deciles and compare their relative strengths of contributions (see Figure 3 ). We note the following in the European context:

Contributions to market beta dispersionsize analysis

Full figure and legend (253K )

Our use of an equal-weighted benchmark should control for any size bias inherent in a ‘standard’ (market-cap weighted) benchmark.

Non-market return compression

Active managers typically focus on the non-market component of stock returns and seek stock-specific alpha opportunities. The decomposition of total return into market and idiosyncratic components allows us to investigate the evolution of the alpha hunting ground for those investors as well. In this section, we focus on the dispersion of non-market returns, _t 2 ( _t ). This metric is particularly relevant for market-neutral strategies.

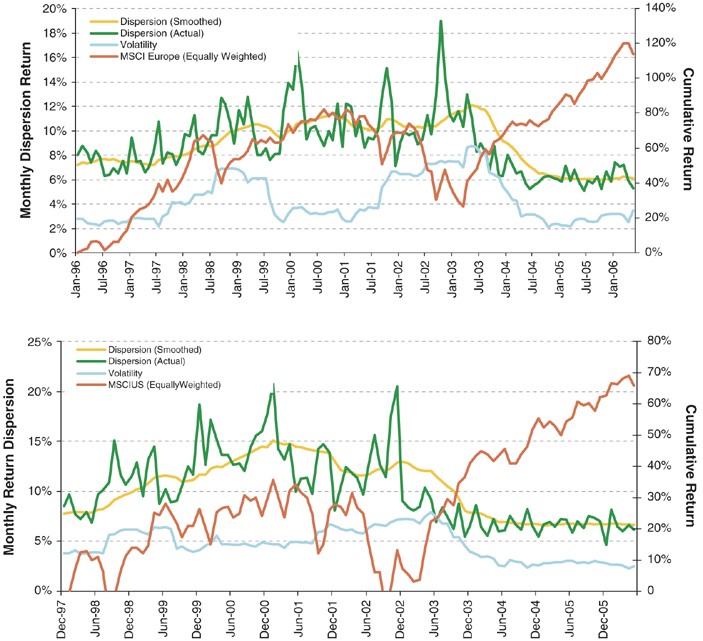
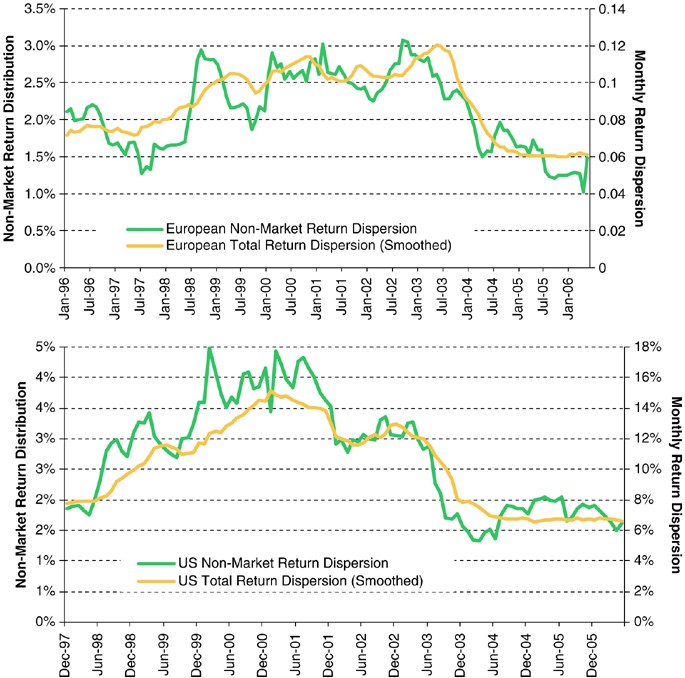
Figure 4 shows the evolution of non-market return dispersion compared to total return dispersion for both Europe and the US. Non-market return dispersion compressed significantly during the market rebound in 2003 and has not recovered since. Combined with the current beta compression, this has led to shrinking of residual return opportunities, particularly during the second part of 2005. Lower than average performance of some hedge funds during that period may well be attributable to this compression. Overall, non-market return dispersion is highly correlated with the total return dispersion. Studying the size and the sources of non-market return dispersion can be helpful in determining the optimal investment approach at any one point in time.

Non-market return dispersion

Full figure and legend (269K )

In the European market, the relative importance of market beta and non-market stock dispersion went through several characteristic episodes during our sample period, which can serve as examples:

• Relatively high non-market dispersion with market beta compression (July to December 1998, July 2004 to July 2005). These periods of decoupling between non-market dispersion and market beta dispersion promise the relatively greater rewards from active stock selection, particularly in a market-neutral setting. Note that the two periods differ in absolute return opportunities the latter period’s opportunity set was much smaller.
• High non-market return dispersion with high market beta dispersion (19992002). These periods of coupling between market and non-market risks require a careful resource allocation between macro (eg tactical asset allocation) and micro (eg fundamental research allocation) stock return drivers. The period encompasses both the latter part of the TMT bull market, where sector effects were important sources of returns, and the bear market following, where optimal market exposure and stock selection were critical.
• Low absolute non-market dispersion with market beta compression (from 2004 onwards). Strong market herding and a lack of residual return opportunities make generating returns from active stock selection challenging, particularly for beta-neutral funds.

Concept of alpha granularity

A measure of alpha granularity, or the ‘availability’ of disparate alpha opportunities, should shed light on the optimal concentration of stocks in the portfolio. Such a measure, however, is often difficult to gauge quantitatively.

Cross-sectional dispersion is closely related to this concept of alpha granularity what proportion of the return potential is generated from a given coverage level. In fact, we can treat dispersion as a hypothetical perfect-foresight scenario, which can serve as an objective benchmark for long/short fund managers.

To see this interpretation, we devise a perfect-foresight portfolio policy as follows:

Let

where

is the unweighted market return.

Written this way, w _it is the amount of money invested in stock i (ignoring the notional amount of proportionality here). Under this assumption, the long or short exposure of each security is directly linked to the subsequent return; as such, the fund size is variable in time according to alpha availability.

Trivially, _{i =1} N w _it =0, namely this is a dollar-neutral ‘hedge fund’.

(ie N times the equally-weighed dispersion).

Hence, the portfolio return is identical to cross-sectional dispersion up to a proportional constant.

Alpha budgeting Country, sector, size, style and beyond

Our dispersion-based analysis of the turbulent equity market environment, ranging from extreme market oscillations to the current relatively low volatility environment, shows that maintaining discipline and a realistic assessment of the risk and return potential is critical. We now use dispersion as our diagnostic tool to investigate the relative importance of different top-down asset classes and the impact this may have on the organisation of an active investment process.

We first revisit the country versus sector debate for European markets. 2 Figure 5 shows the average top-down dispersion across countries and industry groups, as well as the average correlation since 1995. Our results reaffirm our previous conclusions in Europe, since 1998, industry group return dispersion has been consistently higher than that of countries, even though both have declined since 2002. Average correlation has been lower across industry groups than countries since 1998. Return opportunities from industry group allocation are therefore relatively greater than those from country allocation investors should continue to adopt a sector approach to top-down allocation in Europe. 3

Country vs. industry group rotation in MSCI Europe

Full figure and legend (150K )

We can link the top-down dispersion with our earlier total return dispersion metric. This will enable us to introduce the concept of alpha budgeting. We decompose total cross-sectional dispersion in the market into two ‘independent’ components, top-down and bottom-up contribution: