by Daniel J. Burnside

Among those who invest in individual stocks, one of the most commonly misunderstood concepts is that assured diversification can be accomplished with a relatively small portfolio of common stocks. Many people believe that diversification beyond 10 or 20 securities is superfluous despite clear research indicating that the opposite is in fact the case. Even some investment textbooks have helped spread the confusion.

The major reason for the confusion rests with the interpretation of many of the studies that have examined the relationship between the risk of a portfolio and the number of securities that it holds.

In this article, we clarify the previous findings by taking a fresh look at this relationship.

In addition to the misunderstanding of portfolio size and risk reduction, investors need to be aware of an increased need for diversification.

Diversification: Getting Rewarded for Risk

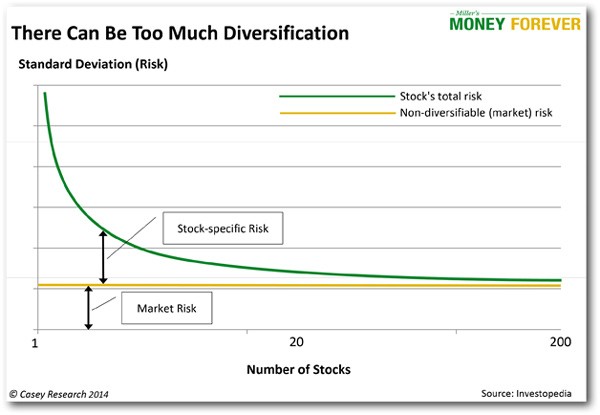
Diversification is an important concept because of the risk-reward relationship. Individual stocks have several kinds of risk, including firm risk, industry risk, and market risk. Firm risk and industry risk are diversifiable risksin a portfolio, they can be substantially reduced by diversifying among different stocks and different industries. Market risk is nondiversifiableall stock portfolios to some degree contain market risk.

An essential point is that diversifiable risk is not consistently rewarded with higher expected returns. On the other hand, bearing overall market risk does tend to be consistently rewarded. Thus, investors with poorly diversified portfolios would be far better off by diversifying those risks and, if desired, taking on the risks that do tend to be rewarded. In other words, by diversifying, you can increase the expected return of your stock portfolio without increasing your risk.

For stock investors, the obvious question that arises from this is: How many stocks does it take to be diversified?

A seminal study addressing this question first appeared in 1968, and most studies since then have followed the same approach.

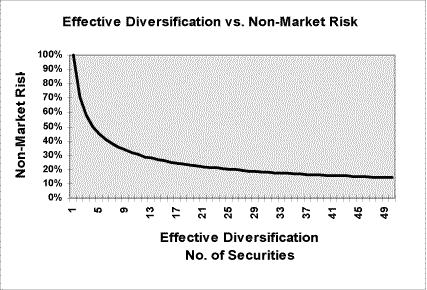
In this early study, researchers formed different-sized portfolios through random selection and observed the risks, as measured by the average portfolio standard deviation. Standard deviation measures volatilitythe amount by which a portfolios actual returns vary around the average return; the more volatile a portfolio, the greater the risk.

The study found that as the portfolio size was increased to roughly 10 stocks, average volatility dropped dramatically. In addition, as the number of stocks increased beyond 10, portfolio volatility continued to drop, but not nearly as dramatically. Subsequent studies have produced similar results.

It is the interpretation of these results that has produced the confusion. A number of researchers have concluded that there are few diversification benefits to justify increasing portfolio sizes much beyond 10 securities.

However, this prescription of relatively small portfolio size stems from the failure to see that investing with an average risk of X percent is not equivalent to investing with a guaranteed risk of the same amount.

For example, a portfolio that has a 50% chance of being risk-free and a 50% chance of having a standard deviation of 20% is less desirable to an investor than a portfolio that is certain to have a standard deviation of 10%, even though both opportunities have the same average standard deviation of 10%.

More recent research has documented that there has been an increasing amount of diversifiable risk contained in stocks. What that means is that the number of stocks necessary to achieve a given level of diversification has actually increased.

Putting together the history of erroneous reasoning regarding adequate portfolio size and the apparent trend of stocks to contain increased diversifiable risk, there is a clear need for an improved understanding of portfolio size and diversification.

How Many Stocks Does It Take?

We undertook our own study that addresses the issue of how large a portfolio should be to achieve adequate diversification.

The Study

Almost all publicly traded equity securities were included in our analysis, which covers the 504 months from January 1960 to December 2001. We computed the returns of randomly selected portfolios with varying numbers of individual stocks, and compared those returns with the returns of a market index. We performed the simulation separately for each of the 504 months, although some results were combined into sub-periods.

In the study, we examined tracking error, which measures the average amount by which the returns of the portfolios deviated from the returns of a target index. We measured the portfolios relative to two target indexes, one a value-weighted market index and the other an equal-weighted market index.