In today’s post, I am discussing the concept of stock’s beta value and how it helps us understand stocks expected returns.

What is Stock’s Beta Value?

In its simplistic form, beta is a measure of any individual stock’s risk (or movement) relative to the overall stock market risk (or movement). Since in Unites States, the overall stock market is represented by S&P500 index, Beta for individual stocks is measured relative to S&P500 index. Now, we can extend this relative measure to monthly returns (instead of price movements). If we compare the monthly return of individual stock to monthly return of S&P500 index, then it helps us put an expectation on our returns.

How to calculate Beta?

The formula for calculating Beta is written as:

Beta = Covariance (stock vs. market returns) / Variance (market)

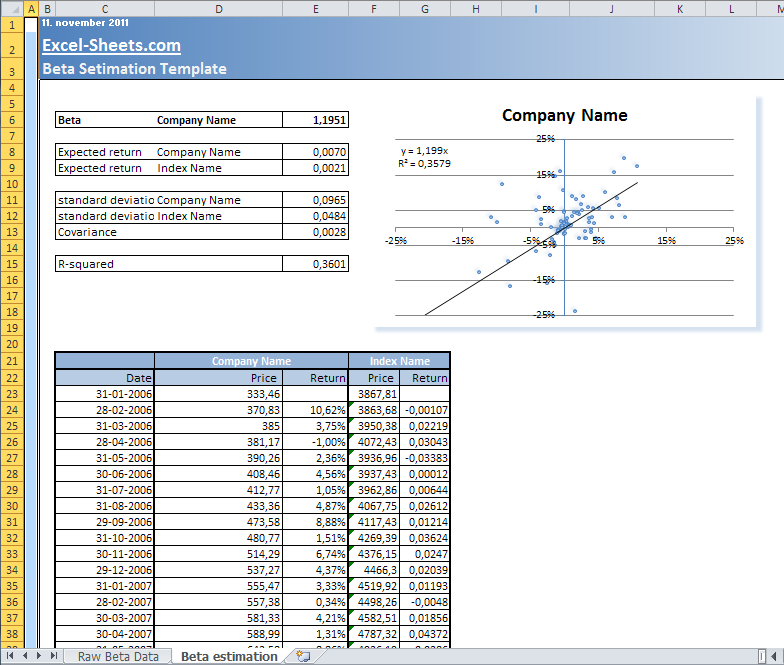
Let us take an example, where we want to calculate the Beta for monthly returns (relative to market). We will calculate 10 year Beta for KMB. We will use a simple linear regression method that can be implemented using Microsoft’s Excel or Google’s spreadsheet. The spread sheet on this link shows the calculations.

Step 1 (Column B):

Download S&P500 index history from January 1998 to December 2008, i.e. monthly closing value. Sort the data in ascending order, such that January 1998 for index and stock are aligned.

Step 2 (Column C):

Download price history from January 1998 to December 2008, i.e. monthly closing price of KMB, from any web portal. I used Yahoo Finance. Sort the data in ascending order.

Step 3 (Column D):

Calculate the monthly returns by (Cell B3 – Cell B2) / (Cell B2). Calculate this until December 2008. Column D will now have monthly returns for past 10 years.

Step 4 (Column E):

Similarly, calculate the monthly returns for KMB in column E.

= covariance (stock vs. market index returns) / variance (market index returns)

= COVAR(E3:E133,D3:D133)/VARP(D3:D133)

= 0.44

Step 6: The Beta value for monthly return for KMB of 0.44.

What this means is the stock of KMB returns 0.44 times the S&P500 index. It can also be interpreted as that volatility (or risk) of this stock is less than market index.

• Beta value greater than 1 – The stock’s price experiences movements that are greater (more volatile and/or risk) than the stock market.
• Beta value less than 1 – The stock’s price movements, or swings, are less than those of the market.
• Beta value equal to 1 – The stock moves in tandem with the market

Now that we know the stock’s Beta value, it can used to calculate the expected return. This calculation is based on Capital Asset Pricing Model (CAPM). It uses risk-free investments, expectations of the stock market, and stock Beta values. While discussing CAPM is a topic in itself, here I am only showing the simple mathematical model. The expected return (ER) is calculated as:

ER = (risk free return) + (Beta) x (expected market return – risk free return)

Where:

• Risk free return – Typically, this is the interest rate one would get from US treasury bills. The 10 year treasury yield is 2.76% during February 2009. I am actually intrigued by the fact that it uses the lowest possible risk free return. Why not use FDIC insured high yielding money market account?
• Beta – it provides stock’s relationship with the market.
• Expected market return – It is the expected market return from a stock market indicator such as the S&P500.  Over the last 15 to 20 years, the general consensus among many estimates is that S&P500 has yielded average annual return of approximately 8%.

In our example for KMB, expected return can be calculated as:

ER = 2.76% + 0.44 x (8.0% – 2.76%)

= 5.04%

What this means is, that the 10 year expected return for KMB stock is 5.04%. What this shows is, with low risk/volatility relative the market comes the stock’s low returns compared to the market.

Few important issues that we need to understand:

In future posts, I will discuss how individual investors can calculate (or develop simple model) the dividend portfolio’s (1) expected dividend growth rate; and (2) Beta-based expected return using individual stock’s characteristics. Stay tuned.