Asset Pricing — May 22, 2013

Understanding the low volatility anomaly

By Lionel Martellini, Professor of Finance at EDHEC Business School and Scientific Director of EDHEC-Risk Institute

There is an interesting discrepancy that exists in the academic literature between the theoretical predictions from standard asset pricing models regarding the risk-return relationship and the results obtained by researchers who have analysed this relationship in equity markets from a purely empirical perspective.

Asset pricing theory, as well as common sense, suggest the existence of a strictly positive relationship between systematic risk and expected return, and a positive or zero relationship between specific risk and expected return.

On the one hand, theory suggests a positive relationship between risk and return. This relationship should be strictly positive for systematic risk measures, and positive or zero for specific risk measures.

Standard asset pricing models first suggest that systematic risk should be (positively) rewarded, that is stocks with higher betas should earn a higher expected return. This prediction applies in both the CAPM single-factor equilibrium model (Sharpe (1964)) and multi-factor models supported by equilibrium arguments (Intertemporal Capital Asset pricing Model, Merton (1973)) or arbitrage arguments (Arbitrage Pricing Theory, Ross (1976)).

While such models predict that investors should not expect to receive a compensation (earn a risk premium) for specific risk, because specific risk can be diversified away, a number of subsequent papers have underlined the explanatory power of idiosyncratic, as opposed to systematic, risk for the cross section of expected returns. In particular, Merton (1987) shows that an inability to hold the market portfolio, whatever the cause, will force rational investors to care about total risk to some degree in addition to market risk so that firms with larger firm-specific risk require higher average returns to compensate investors for holding imperfectly diversified portfolios (see also Malkiel and Xu (2006) or Barberis and Huang (2001)).

In closing, academic theory suggests that systematic volatility should be positively rewarded, and that specific volatility may be positively rewarded, or earn no reward (which is obviously different from saying it should earn a negative reward), depending on underlying assumptions.

Empirical analysis, however, has unveiled evidence of a negative risk-return relationship in equity markets.

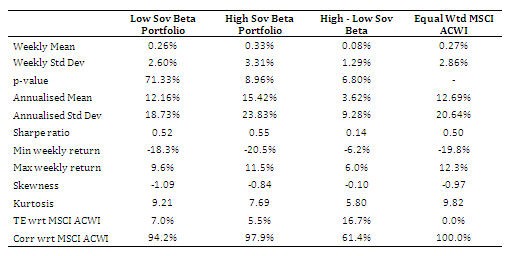
On the other hand, a number of older as well as more recent papers have reported a series of puzzling, or at least, contrasted findings from an empirical perspective. First, the “low beta anomaly” stipulates that the relationship between systematic risk as measured by a stock beta and return is much flatter than predicted by the CAPM (see early papers by Black (1972), Black, Jensen, and Scholes (1972), as well as Haugen and Heins (1975), who claims that the relationship was not merely flat in their sample period, but actually inverted).

More recently, Ang, Hodrick, Xing, and Zhang (2006, 2009) have drawn new attention to these results with a focus on the specific risk component, finding that high idiosyncratic volatility stocks have had abysmally low returns in longer U.S. samples and in international markets. This result is now widely known as the “idiosyncratic puzzle” or “iv puzzle” in short. Yet other papers have documented a rather flat or even negative relationship between total (as opposed to specific) volatility and expected return, an anomaly that some call the “total volatility puzzle”, or “tv puzzle” in short.

In early work, Haugen and Heins (1972, 1975) analyse pitfalls in commonly used cross-sectional tests of the risk-return relationship, and express doubts regarding the existence and significance of the risk premia implied by standard asset pricing models. In a more recent study, Haugen and Baker (1996) find a positive or negative average payoff to total volatility in the cross section of stock returns depending on the dataset under consideration (see also Haugen and Baker (1991, 2010) for related results). Blitz and van Vliet (2007) analyse a twenty-year period and show results in which portfolios of low-volatility stocks have higher returns than portfolios of high-volatility stocks, albeit without reporting significance levels. Similarly, Baker, Bradley, and Wurgler (2011) find that portfolios formed by sorting stocks by past volatility display higher returns for the low-volatility quintile over the subsequent month than for the high-volatility quintile. Finally, Bali, Cakici, and Whitelaw (2011) investigate a measure of lottery-like return distributions, which is highly correlated with other risk measures, and find that it is also associated with poor performance.

Recent research has proposed a number of attempts to explain, or explain away, the volatility puzzle.

That we are left with such a puzzling picture regarding the exact nature of the risk-return relationship, and that we do not have a clear idea regarding whether it is positive, flat or even negative, is rather surprising, and somewhat embarrassing, given that a fair understanding of this question is of central importance in both asset pricing theory and investment practice. Fortunately, a number of recent papers have tried to provide various insights into these puzzling empirical findings. Broadly speaking, there are two types of explanations of the volatility anomaly in the literature, which can be classified, respectively, as (i) attempts to explain the puzzle, i.e. attempts to find economic reasons that explain why a negative relationship might exist between some risk measure and expected returns, versus (ii) attempts to explain it away. i.e. attempts to argue that these empirical findings are not robust in the first place, and may simply disappear when slightly different methodological choices are made when conducting the empirical investigations.

Regarding economic explanations behind some of the empirical puzzles, it is for example now well understood that the “low beta anomaly” is not an anomaly, but instead a mere indication that the cross-section of stock returns is poorly explained by a single-factor model such as the standard CAPM. For example, while Fama and French (1992) find that, while the relationship between a stock beta with respect to the market portfolio and the stock average return was not significant, stocks with high exposure to the size and/or B/M factor do earn a higher expected return, in accordance with the predictions of standard asset pricing models. Turning to the volatility puzzle, one possible explanation relates to investors’ preference for lottery-like payoffs obtained with high-volatility stocks and limit to leverage (see in particular Baker, Bradley and Wurgler (2011)). According to this explanation, the high demand for high volatility stocks by investors deviating from the mean-variance paradigm implies that the prices of such stocks is driven up, hence generating lower expected return. A related explanation relates to the existence of institutional limitation on using leverage (Baker, Bradley and Wurgler (2011)). Hence, risk-tolerant investors who seek to implement highly aggressive strategies would optimally opt for a leveraged investment in the maximum Sharpe ratio portfolio. Because of the presence of leverage constraints, such investors would instead overweight high volatility stocks in an attempt to spend their risk budget. This increased demand for high volatility stocks leads to increases in prices for these stocks, and explains again their low performance.

Alternatively, another set of papers have provided evidence that these empirical findings are not robust in the first place, and may simply disappear when slightly different methodological choices are made when conducting the empirical investigations. Hence, a number of recent papers have questioned the robustness of Ang et al. (2006, 2009) results and have therefore questioned the mere existence of the volatility puzzle. Among other concerns, the findings are not robust to changes to data frequency, portfolio formation, portfolio weighting scheme (cap-weighted versus equally-weighted) to the screening out of illiquid stocks (Bali and Cakici (2008)) or to past maximum returns (Bali, Cakici, and Whitelaw (2011)). The use of geometric versus arithmetic averaging for portfolio return has also been found to have a strong impact on the result.

Other authors change the short-term measure of volatility in Ang et al. (2006) with measures obtained over longer horizons and then find a positive relationship (Fu (2009), Spiegel and Wang (2005), Brockmann and Schutte (2007), Eiling (2006)). In a related effort, Cao and Xu (2010) decompose idiosyncratic volatility into its short- and long-term components and find a positive relationship between the long-term component and expected stock returns. The most popular explanation might be the one related to the existence of short-term reversals. Indeed, the empirical underperformance of high volatility stocks tends to be concentrated in the highest decile, and a careful analysis unveils that most of the stocks in that decile for one particular sample period have enjoyed a strong rally in the calibration period. A short-term correction usually occurs after the rally has taken place, hence explaining why the one-month horizon performance of the highest volatility stocks tend to be poor subsequently to the identification of these stocks having enjoyed a substantial increase in prices. Hence, or to Huang et al. (2010) finds that the low volatility anomaly disappears after adjusting for such short-term return reversals. More generally, it appears that the risk-return relationship seems to become more and more positive as intuition suggests as the holding horizon increases (see Huang et al. (2011) for holding periods of 12 months, or Goltz and Martellini (2013) for holding periods up to 60 months).

Low volatility strategies can be useful, regardless of whether or not one believes in a positive, or negative, risk-return relationship.

The debate about the low volatility puzzle has important practical implications. Different priors, such as all stocks have the same expected returns, or more risky stocks have lower expected returns or more risk stocks have higher expected returns, will indeed lead to different proxies for the optimal tangency portfolio every rational risk-averse investors will want to hold according to modern portfolio theory. Overall, that empirical results are not robust with respect to methodological choices should be taken as an indication that analysing the exact shape and nature of the risk-return relationship is a subtle question that requires extreme care and attention.

References: