Portfolio Management — November 15, 2011

Advantages and shortcomings of minimum variance portfolios

By Stoyan Stoyanov, Professor of Finance, EDHEC Business School, and Head of Research, EDHEC Risk Institute—Asia, and Felix Goltz, Head of Applied Research, EDHEC-Risk Institute

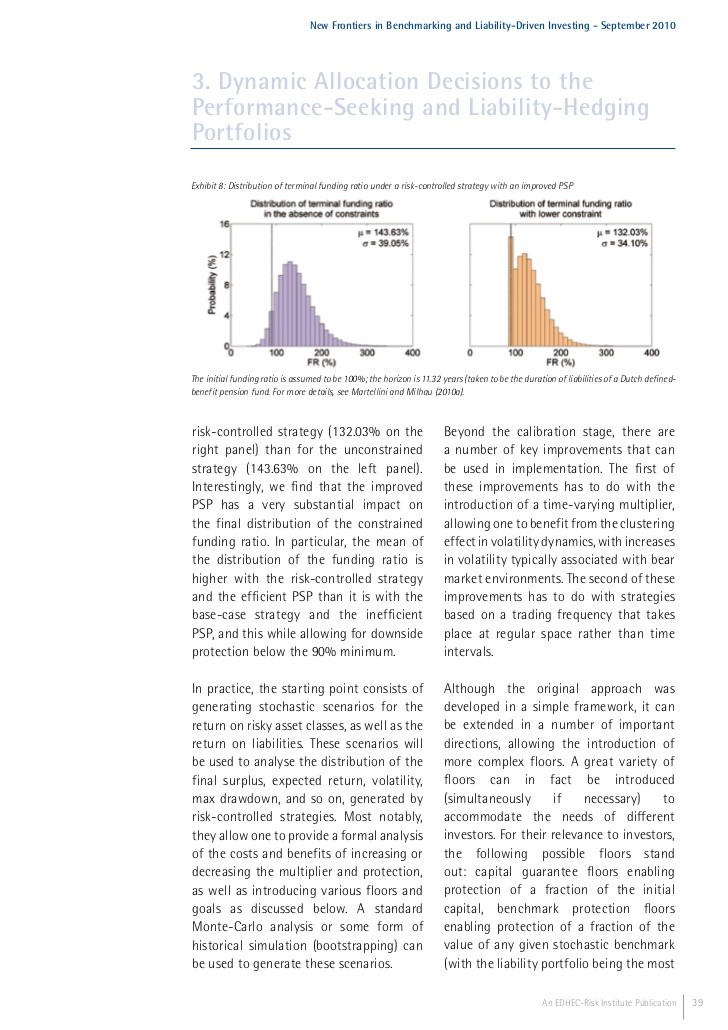
Since minimum variance portfolios have only the objective of lowering risk, rather than aiming to optimise the risk/reward ratio, minimum variance portfolio optimisation leads to a pronounced concentration in low volatility stocks at the expense of exploiting correlation properties. While minimum variance portfolios are not optimal portfolios, they may be suitable for investors who wish to load up on low-risk or ‘defensive’ stocks.

Scientific diversification is based on reaching a high risk/return objective through portfolio construction techniques. It corresponds to the desire of investors to position their portfolios on the efficient frontier of Modern Portfolio Theory. Approaches based on scientific diversification are increasingly being used to construct equity core portfolios in institutional investment management, with the aim of gaining an optimal risk-reward profile from exposure to equities.

In practice, to obtain a decent proxy for efficient portfolios, one needs to use careful risk and return parameter estimates. In essence, practical approaches to equity portfolio construction based on scientific diversification make different choices regarding the challenge of risk and return estimation.

The global minimum variance (GMV) portfolio is a remarkable portfolio providing the lowest possible portfolio volatility. This means that the only required optimisation inputs are correlations and volatilities. Since estimation risk inherent in expected returns is well known, the fact that the minimum volatility portfolio relies only on risk parameters is an appealing feature (see for example Amenc and Martellini (2002) among many others who have made this argument). To be sure, estimating risk parameters is also a serious challenge, with issues such as the “curse of dimensionality” when dealing with a large number of assets as well as the “curse of non-stationarity” of risk in the stock market. However, ever since Markowitz published his theory of “portfolio selection” in the 1950s, constant progress has been made on dealing with these challenges and today there is a rich set of tools at our disposal that allows improving risk estimates, including sophisticated factor models as well as dynamic risk models.

Despite the reasonable idea of avoiding expected returns estimation, minimum variance portfolios have been shown to lead to underdiversified portfolios. DeMiguel, Garlappi and Uppal (2009) for example evaluate a range of minimum variance portfolios across seven empirical datasets, and they find that none is consistently better than a simple equal-weighting rule in terms of Sharpe ratio.

In addition to such empirical findings, there are two main interrogations with minimum variance portfolios. From an ex-ante perspective, minimum variance portfolios are not optimal portfolios. They will be dominated by a combination of the risk/reward optimal portfolio (tangency portfolio) with cash. In principle, investors should only care about designing this tangency portfolio, using cash holdings if they wish to reduce their portfolio’s volatility to a lower level. This tangency portfolio will only coincide with the minimum variance portfolios if one is ready to assume that expected returns of all assets are identical, clearly a strong and rather unrealistic assumption.

From an ex-post perspective, standard minimum variance portfolios are typically heavily concentrated in the assets with the lowest volatility. The high concentration in GMV portfolios is a widely recognised issue. Clarke, De Silva and Thorley (2011) note that their long-only minimum variance “portfolio averages about 120 long securities, i.e. about 12% of the 1000-security investable set”. Likewise, DeMiguel et al (2009) note that “shortsale-constrained minimum-variance portfolios […] tend to assign a weight different from zero to only a few of the assets.”

It is interesting that the high concentration property of GMV portfolios is by no means empirical in nature and this can be demonstrated by a simple model. First, assume that stock returns are not correlated. Then, it is a theoretical fact that the weights of the GMV portfolio are inversely proportional to the corresponding variances. As a consequence, a stock with volatility twice as high as the volatility of another stock will have a four times smaller weight in the GMV portfolio.

Assuming an average correlation higher than zero does not improve concentration. In fact, it only exacerbates the problem (see Amenc et al (2011)). To illustrate this phenomenon, consider a hypothetical universe of 100 stocks with annualised volatilities equally spaced in the following ranges: [16%, 18%], [15%, 19%], [13%, 21%], and [10%, 24%]. In the four cases, the average volatility is the same; the only difference is the dispersion of the volatilities around the average. We can calculate numerically the GMV long-only portfolios assuming for simplicity equal correlations ranging from 0% to 99%. To measure the degree of concentration, we use the inverse of the Herfindahl index: the inverse of the sum of squared weights (see, for example, Malevergne et al (2009)). For an equally weighted portfolio, the concentration metric is equal to the number of stocks and, for a totally concentrated portfolio, it is equal to one. This concentration metric is also referred to as the effective number of stocks.

Concentration of long-only GMV portfolios as a function of correlation in a constant correlation model (top) and the sum of the GMV weights corresponding to three groups of stocks of equal size ranked by their volatility for the case of equally spaced volatilities in [16%, 18%] (bottom).

20Investments/RISKArticle.2005-01-11.4331/images/minvol1.jpg /% 20Investments/RISKArticle.2005-01-11.4331/images/minvol2.jpg /%

The plot of the effective number of stocks as a function of correlation is provided on the top plot in the figure. As expected, the relationship is monotonic in the four cases – bigger correlation implies higher concentration. Also, all other things being equal, a wider range of volatility corresponds to greater concentration.

The top plot in the figure indicates that concentration increases, but it is not clear if it does so as a result of the higher relative weight of the low-volatility stocks. To explore this question, we rank the GMV stocks into three groups of equal size and then calculate the sum of the weights of the stocks in each group. The bottom plot in the figure shows the sum of these weights as a function of correlation, assuming that the stock volatilities are in the interval [16%, 18%]. If the stock returns are non-correlated, the total weight allocated to the three groups of stocks is almost the same, which is consistent with the effective number of stocks being near 100 on the left plot. As correlation increases, the total weight allocated to the lower-volatility stocks increases monotonically, an increase that is offset by a monotonic decrease of the total weight allocated to the group of higher-volatility stocks. For correlation greater than 0.6, the portfolio is concentrated entirely in the group of lower-volatility stocks.

Irrespective of whether low volatility stocks are attractive or unattractive, it is clear that a minimum variance strategy leads to poorly diversified portfolios and does not fully exploit correlations. In fact, the theoretical model suggests that correlations are exploited only to increase concentration further in the low volatility stocks. This is not strange bearing in mind that the objective is to minimise variance and not concentration but this fact is an important side effect to be taken into account as far as diversification goes. In the end, for investors who have made the decision to move away from market-cap-weighted portfolios one can reasonably question whether replacing the concentration in the largest capitalisation stocks inherent in cap-weighting with concentration in the lowest volatility stocks addresses their concerns.

In fact, a number of practitioners have proposed a rationalisation of minimum variance strategies which builds on the argument that this concentration in low volatility stocks will help increase performance. However, in light of such an argument, two remarks are in order.

First, the idea that low volatility stocks come with higher expected returns is far from a consensual finding. While there are findings that low volatility stocks come with higher returns (Ang, Hodrick, Ying, and Zhang (2006), these findings have been shown to lack robustness when changing the data frequency, portfolio formation, screening out illiquid stocks (Bali and Cakici 2008), or adjusting for short-term return reversals (Huang et al. 2010). Other authors have introduced improvements when measuring stock volatility and they find that low volatility stocks have lower returns (see in particular Fu 2009). Amenc et al. (2011) show that the investment horizon has a strong influence on the risk-return relationship. In particular, the volatility anomaly that high volatility stocks have low returns disappears for holding periods greater than one year.

Second, even if one sees low volatility stocks as attractive, notably in terms of enabling the construction of defensive portfolios which will display a tendency to perform well in times of downward market direction, one should not lose sight of the fact that it is desirable to hold well-diversified portfolios. One should be careful to avoid confusion between low volatility portfolios, which achieve some risk reduction while maintaining a fair degree of diversification, and highly concentrated minimum volatility equity portfolios, which will be highly exposed to sector-specific or stock-specific risks.

Researchers have recognised this limit of minimum volatility portfolio construction, and have proposed various ways to remedy the concentration of optimised portfolios in low volatility stocks. The most straightforward solution to any concentration problem is to impose weight constraints. Imposing lower and/or upper bounds on weights provides quite rigid constraints which leave reduced room for optimisation, but can help to obtain more reasonable portfolios. Recently, more flexible weight constraints have been proposed by DeMiguel, Garlappi, Nogales, and Uppal (2009), who use so-called “norm constraints.” Such constraints put limits on the overall amount of concentration in the portfolio (e.g. on the sum of squares of portfolio weights) rather than limit the weight of each stock in the portfolio, thus leaving more room for the optimiser while avoiding concentration overall. An alternative to the use of weight constraints is to avoid making a difference between stocks based on their volatilities. Christofferson et al (2010) minimise volatility with the assumption that volatilities are identical across stocks. Hence the only differences across stocks that the optimiser then takes into account are differences in correlations. The minimum volatility portfolio under this assumption will thus be unaffected by a concentration in low volatility stocks, at the cost of an implicit assumption that all volatilities are equal.

A different way of avoiding excessive concentration in low volatility stocks is to penalise these stocks in the portfolio optimisation. Amenc et al (2010) construct efficient indices and benchmarks by maximising the Sharpe ratio, rather than minimising volatility. The approach effectively penalises low risk stocks through assuming a positive long-term relationship between risk and return. This penalty on the expected returns side counterbalances the attractiveness of low risk stocks from a risk perspective. To ensure parsimony and robustness, they group stocks by their total downside risk (in particular a stock’s semi-deviation, which incorporates higher moments) and distinguish stocks based on their riskiness only across groups rather than on a stock by stock basis.

The important insight that carries through from Markowitz’s early work on efficient diversification to recent work on portfolio construction is that while portfolio returns are a simple weighted average of component returns, the portfolio volatility is not just the weighted average of the stock’s volatilities. For a given level of return, one can lower the risk by intelligently combining stocks according to their correlations. Since GMV portfolios have the only objective of lowering risk, they exploit correlations only to the extent that this objective is achieved. Such portfolios are therefore suitable for investors who wish to load on low-risk or “defensive” stocks, while alternative approaches may be relevant for investors who want to manage risk and reward properties through combining both low risk and high risk stocks in a broadly diversified portfolio.

References

papers.ssrn.com/sol3/papers.cfm?abstract_id=1458280