Diversification is the process undertaken by investors in order to reduce risk via investments in an assortment of assets. The idea of diversification has been around for a long time, dating back to 935 B.C. where in the Hebrew bible it quotes “But divide your investments among many places, for you do not know what risks might lie ahead”.

Harry Markowitz, a respected economist and Nobel Prize winner, in 1952 introduced modern portfolio theories that we are still familiar with today with regards to diversification for efficient portfolio management. The primary aim of modern portfolio theory is to maximise returns for a given level of risk, or alternatively, to reduce risk for a given level of return. Work by Markowitz led to the development of the “Capital Asset Pricing Model”. This model suggests that there are two types of risks: diversifiable and non-diversifiable. Diversification is an important factor to consider for risk averse investors. Such investors are assumed to be rational, meaning they would like to maximise returns whilst minimising risk.

2.1. Aims

This paper primarily focuses on international markets; we aim to investigate to following matters:

To distinguish the level of international diversification that is required to optimise returns,

Assess the implication of recessions on the diversification process,

3. Literature Review: (current word count: 2685)

The Literature review is split into three section; the first documents studies focused on domestic diversification, the second documenting studies on international diversification and the final section looking at studies investigating diversification during recessions.

3.1. Studies on domestic diversification

There have been several influential studies in relation to portfolio selection; a revolutionising paper in this field was by Markowitz (1952) in which he introduced the “Mean-Variance approach” (MV). He suggested the following equations for optimal portfolio construction: (Equation 1: Expected return of a portfolio; Equation 2: Variance of a portfolio)

Equation 1 Equation 23

Markowitz states that the foremost determining factor for ‘good diversification’ of a portfolio is the covariance between stocks as opposed to the quantity of stocks held, thus covariance is included in the variance calculation (Equation 2); a lower correlation reduces the variance, the predominant idea behind the MV approach is the minimisation of portfolio variance.

The study by Markowitz is focused on one-period analysis; however, numerous researchers have argued that investors should hold portfolios for a greater number of years. Latané (1960) stated that the probability of an investor achieving the highest level of utility is strongest when the number of years that a portfolio is held for nears infinity. This implies that the rational investor is more likely to achieve the expected return for the securities he is holding given that they have been held for a long period of time. Thus concluding in his study that whilst constructing portfolios, investors must consider the expected geometric return. Elton and Gruber (1974) agree with Latané, they state that the expected geometric mean allows identification of portfolios generating the highest expected utility of terminal wealth.

Since Markowitz, there have been several studies with regards to portfolio selection, one that is consistent with the theories behind Markowitz and the benefits gained from diversification is by Evans and Archer (1968). They examined the reduction in risk of portfolio returns whilst increasing the quantity of securities. Their study was based on semi-annual observations from 470 securities listed on the “Standard and Poor’s Index” between January 1858 and July 1967. Evans and Archer generated 40 portfolios; firstly they extracted one security out of the 470 at random, computed its return and standard deviation, and thus produced a portfolio containing one security. This process was replicated, i.e. for the second portfolio, a selection of two securities was made, one from the remaining 469 and one from the original listing of 470 securities. The method of generating these 40 portfolios was then reproduced a further 60 times, the resultant being 2400 portfolios, each with its own standard deviation and mean return. The results they observed indicated that the majority of unsystematic risk was removed on the addition of the 8th security. Further risk reduction was possible, however, it required a substantial increase in the quantity of securities added to the portfolio. Further to this, results showed that the benefit gained beyond 19 securities was minimal. The observed standard deviation value dropped by 55% as number of securities increased from 1 to 40; this allowed them to conclude that there is existence of a relationship between the quantity of securities held and the dispersion of that given portfolio.

As discussed previously, one of the most widely respected theories is the MV approach, however this method faces drawbacks; one being that the optimum portfolios suggested by the model have tendencies to contain heavy concentrations on a few assets. Bera and Park (2008) stated that this problem is due to statistical errors with the input estimations required for the MV method. To overcome this, they implemented the cross-entropy (CE) method developed by Reuven Rubinstein through use of the Monte Carlo approach. The CE method, also recognized as the Kullback-Leibler information criteria is defined as “a measure between two probability distributions (i.e. two portfolio weights; “p and q”), which in nature is non-symmetric)”. (Kullback and Leibler, 1951)

Equation 3

Bera and Park examined eight international equity indices (US, UK, Canada, Italy, Japan, Switzerland and Germany) extracted from data supplied by Morgan Stanley Capital International. In order for performance analysis of the portfolios, they used a “rolling window” scheme; this allowed them to obtain portfolio returns for the next period. The empirical results obtained in this study indicated that there was superiority to the MV approach in the portfolio selection process when the CE measure was implemented. The two main reasons they suggested this superiority is due to the freedom in portfolio weighting and the possibilities of immediate extension for the incorporation of greater moments e.g. asymmetry.

A more recent study by Miller and Scholes (1972) has divulged evidence on the existence of positive correlations between market and non-market risk of individual common stocks. In the case of such a relationship being present, the diversification process would be influenced by the quantity of securities in a portfolio as well as the average beta coefficient of the portfolio. A study by Klemkosku and Martin (1975) addressed this issue, they aimed to test this relationship and determine the significance of it on the diversification process.

Klemkosku and Martin assessed 350 individual common stocks from the New York Stock Exchange on a monthly basis between June 1963 and June 1973; the beta coefficients were then calculated via regressions analysis. This allowed them to make approximations on the percentage price change via stock price logarithms, all on a monthly basis. They stated that the measure of variation about the regression outputs would be via the residual risk, which is displayed through squares of the standard errors. Results obtained indicated that portfolios with a higher beta value required a greater quantity of securities in comparison to portfolios with a lower beta in order to achieve the same level of diversification. This is an important factor to consider for an individual who seeks to maximise the benefits of diversification but limit the amount of securities held.

Whilst analysing the benefits associated with diversification, it is common to evaluate correlations amongst the investments; this is primarily due to the common knowledge that diversification benefits decline with increasing correlations. However, Statman and Scheid (2008) claim that comparison via correlations is not a good indication of diversification benefits. The two reasons they give to back this statement are firstly, because correlation is not an intuitive indicator, and secondly diversification benefits are not entirely reliant on correlations, there is also dependency on the standard deviation of returns. An alternative measure suggested is via return gaps, return gaps are superior since they account for both the standard deviation and correlation between two securities, thus will provide an intuitive measure of diversification benefits. Statman and Scheid focused their study around measurement via return gaps and attempted to determine the difference between the two measures discussed. Results they obtained showed that for a given set of assets ordered by the benefits of diversification, a significant difference of that particular order was noticed when the two different methods of measurements were implemented.

3.2. Diversification into international markets

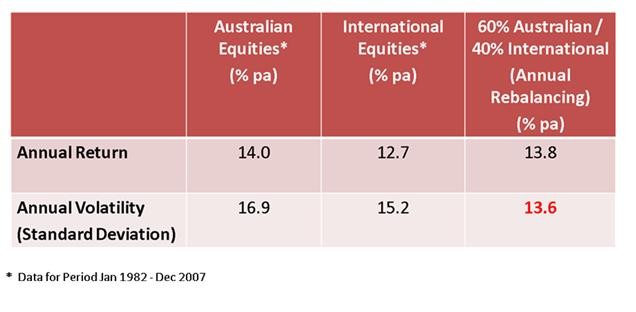
Levy et al (1970) aimed to show that diversification into international markets can induce further benefits. The study involved the calculation of mean rates of returns and their corresponding standard deviations from 28 countries on an annual basis between 1951 and 1967. Results obtained showed that as a greater level of international diversification was implemented, the standard deviations of the average rate of returns declined. Thus implying that a lower risk is associated with greater international diversification.

Solnik (1974) produced results consistent to those by Levy. The initial idea brought forward by him is that the risk of a portfolio is not solely dependent on the number of securities within it, but also by the individual risks of those securities. Solnik sampled 300 European stocks, taken from The Netherlands, Belgium, Italy, Switzerland, France, Germany and the United Kingdom; all taken during 1966 and 1971. Within each country, Solnik generated similar sized portfolios consisting of ascending stock types; and then measured the risk of each portfolio as means of comparison. Results showed that there was a disproportionate decrease in risk with greater diversification. When diversification is expanded into international markets there are significant reductions in risk, primarily due to the independence of different stock markets. The study revealed that return on a suitably diversified international portfolio would be ten times less risky in terms of variability when compared to typical securities. Furthermore, it would be half as risky as a well-diversified domestic portfolio (US stocks were used in this analysis).

Further to this, Solnik mentioned the presence of exchange risk, this is the risk experienced due to varying exchange rates that can potentially affect the value of investments; a solution to overcome this would be via the hedging of the foreign investments.

Several studies that exemplify the gains of diversification into international markets have been conducted since the work of Solnik; such studies include those by Errunza (1997), DeSantis and Gerrad (1997), and Stulz (1997).

The benefits of international diversification have been well documented; consequently, this has led to a greater integration of international markets, which has resulted in higher correlations between them. Thus, in terms of risk, international investments can prove to be dangerous. Longin and Solnik (1995) conducted a study into stock market indices from 1960 to 1990. The results they obtained indicated instabilities in international covariance and correlation matrices. Further studies have shown that these correlations are even greater during higher economic and financial integration. Based on this work, a study by Eun et al (2008) looked at how small-cap stocks could be used as a driving mechanism for international portfolio diversification. Their findings indicated significant benefits for investors if they opted into investing in small-cap stocks.

An interesting issue that arises within international portfolio diversification is whether the benefits gained are consistent regardless of the investors’ home country. Previously, smaller countries tended to face restrictions on investments so that benefits were received in their home economy, in these present times governments of such countries have eased up on such restrictions, thus giving investors greater freedom. Driessen and Laeven (2007) conducted a study that aimed to investigate the benefits of diversification from different countries from an investor’s point of view. Their work was in continuation of that by Huberman and Kandel (1987), Bekaert and Urias (1996), De Roon et al (2001), and Li et al. (2003). Driessen and Laeven start by stating how international diversification for U.S investors does not show a large amount of benefits (measured via the MV approach) in comparison to investors in developing countries or smaller countries. This was consistent with the results they obtained; they sampled 23 developed countries and 29 developing countries. They noticed that when international diversification was applied, the Sharpe Ratio increase is 13.5% in developing countries, yet in developed countries it only increased by 7.8%. The Sharpe Ratio (S) measures the “reward-to-variability ratio” (W. F. Sharpe, 1994):

Equation 4

The greater the Sharpe ratio, the greater the return for a given risk, thus Driessen and Laeven were able to show that diversification benefits are greater for developing countries. Another aspect they uncovered was that diversification benefits had a linear relationship to the risk of a country; greater potential benefits were associated with riskier countries.

Further studies in international diversification have shown that although investments in developed markets are generally associated with less risk, investments in emerging markets can produce returns that compensate for the risks associated to them, thus a diversified portfolio should contain investments from both developed and emerging market equities. Beach (2006) based a study on this aspect and aimed to show why emerging market equities should be part of well-diversified portfolios. Fender (2002) who motivated Beach’s study explains, “Why International Equities belong in a Diversified Investment Portfolio”. In order to determine whether emerging market equities are a suitable investment option, Beach examines the risks induced corresponding to their returns when such equities are contained in a portfolio. Measurement of risk is carried out via standard deviation, semi-deviation, beta, as well as downside betas. Beach used the Capital Asset Pricing Model (CAPM) in his analysis and discovered that when investing in an emerging market index a return of 1.27% per month is provided compared to a significantly less return of 0.775% per month in an developed market index. Further to this, the emerging market index contained a Sharpe ratio of 0.1282 compared to the 0.087 of the developed market index.

A similar study by Kim and Singal determined that the returns gained from a globally diversified portfolio containing investments from emerging markets was justified by the risks associated to those markets; their study was conducted from the perspective of U.S. investors. Hence, it is suitable to say that when an investor is constructing an international portfolio, he should include an emerging market index within it since they compensate for their risk levels by providing greater rates of returns.

3.3. Diversification during financial shocks

Another fascinating topic that arises within portfolio diversification is the behavior of investments in periods of economic uncertainty. There have been several points in history where extensive shocks have hit the financial markets, a few of these being the 1987 stock market bubble, the dot-com bubble, the Long-Term Capital Management, and of course the most recent “Credit Crunch”. During these periods of crises there have been severe declines in equity markets, greater credit spreads, drastic drops in the confidence of financial institutions, greater asset volatility and very high levels of risk aversion. Goldwhite (2009) examined the behavior of investments in high volatility periods via analysis of the VIX. The VIX is a measure of volatility of the S&P 500. Goldwhite demonstrated that VIX could be a suitable categorisation method for investments. His study compliments the work by Szado (2009), who addressed the following question in his study: “What could have been done to ensure that the effectiveness of a portfolio’s diversification survived in such an environment?” The study was conducted between March 2006 and December 2008; the time frame covered was shortly after the establishment of the VIX. The performance of the portfolios constructed by Szado showed that there was an insignificant increase in diversification benefits with the addition of bonds and other assets. This was the case shortly after the “Credit Crunch” during the second half of 2008. However, the performance of VIX observed was solid, thus showing the addition of VIX futures to base portfolios can induce diversification benefits.

A further study similar to those by Szado and Goldwhite was by Odier and Solnik (1993). Results they obtained indicated that in periods of declining markets, the correlations of U.S and international markets were significantly higher in relation to those of rising markets; it is common knowledge that with higher correlations are related to lower benefits from diversification. This shows us that even though diversification is essential in time periods of falling markets, the gains are minimal.

4. Data and Methodology

Financial theory suggests that there are two types of risks associated with securities: systematic and unsystematic. Systematic risk is associated with the market whereas unsystematic risk is associated to the specific security; the purpose of diversification is to reduce the later risk type.

We can already distinguish from previous studies mentioned in the literature review that diversification can be highly beneficial for rational investors. In this study I will be investigating how the benefits of international diversification can be experienced at different points in time; I will be considering a time frame of 15 years; between 1st January 1995 and 15th November 2010. Previous studies have documented the level of diversification required within the domestic country in order to optimise returns, in this study we will be focused on international markets. The primary aim is to distinguish the level of international diversification that is required to optimise returns and to determine which time periods it would be most beneficiary to undertake the diversification process.

4.1. Data

The data type I will be using in this analysis will be market indices, data has been extracted from Yahoo Finance for the following indices on a daily basis: FTSE 100 (UK), S&P 500 (US), Hang Seng (Honk Kong), CAC 40 (France), DAX (Germany), BEL 20 (Belgium), Bovespa (Brazil), ATX (Austria), IPC (Mexico), AEX (Netherlands), Nikkei 225 (Japan), and the STRIATS TIMES INDEX (Singapore). The selection of these major indices is appropriate in that they can be used as proxies for smaller indices.

4.2 Returns, Correlations and Risk

From market prices, percentage return for individual trading days is calculated via Equation 5. The value obtained shows the capital gains achieved from the given index. In this equation, we are assuming absence of dividend payments; in reality actual received returns from a market index is the summation of capital gains and dividend payments. In this study we aim to investigate how investing in different markets can be an optimum investing strategy, thus it is safe to ignore dividend payments and focus on the market itself.

Equation 5

From this, correlation coefficients (summarised in Figure 1) between different indices are calculated for the period between 1st January 1995 and 15th November 2010. The correlation coefficient aims to measure the linear strength between two assets, for example between A and B, see Equation 6. The value is standardised due to the inclusion of standard deviations. It’s output ranges from -1 to 1; -1 indicating a perfect negative correlation, indicating the return between the given assets move in opposite directions. Alternatively a value of 1 shows perfect positive correlation, thus indicating return between the given two assets move together in the same direction. On the other hand, a correlation value of 0 indicates that the return between the two given assets is completely independent.