Break-Even Method of Investment Analysis

by P.H. Gutierrez and N.L. Dalsted * (3/12)

• A break-even point defines when an investment will generate a positive return.
• Fixed costs are not directly related to the level of production.
• Variable costs change in direct relation to volume of output.
• Total fixed costs do not change as the level of production increases.

Break-even analysis is a useful tool to study the relationship between fixed costs, variable costs and returns. A break-even point defines when an investment will generate a positive return and can be determined graphically or with simple mathematics. Break-even analysis computes the volume of production at a given price necessary to cover all costs.

Break-even price analysis computes the price necessary at a given level of production to cover all costs. To explain how break-even analysis works, it is necessary to define the cost items.

Fixed costs, incurred after the decision to enter into a business activity is made, are not directly related to the level of production. Fixed costs include, but are not limited to, depreciation on equipment, interest costs, taxes and general overhead expenses. Total fixed costs are the sum of the fixed costs.

Variable costs change in direct relation to volume of output. They may include cost of goods sold or production expenses such as labor and power costs, feed, fuel, veterinary, irrigation and other expenses directly related to the production of a commodity or investment in a capital asset. Total variable costs (TVC) are the sum of the variable costs for the specified level of production or output. Average variable costs are the variable costs per unit of output or of TVC divided by units of output.

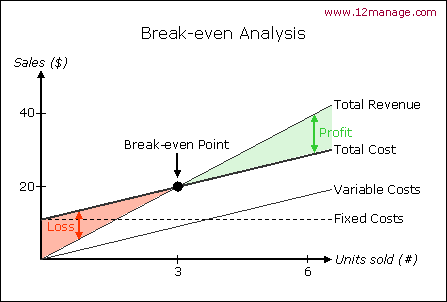
Total fixed costs are shown in Figure 1 by the broken horizontal line. Total fixed costs do not change as the level of production increases. Total variable costs of production are indicated by the broken line sloping upward, which illustrates that total variable costs increase directly as production increases.

The total cost line is the sum of the total fixed costs and total variable costs. The total cost line parallels the total variable cost line, but it begins at the level of the total fixed cost line.

The total income line is the gross value of the output. This is shown as a dotted line, starting at the lower left of the graph and slanting upward. At any point, the total income line is equivalent to the number of units produced multiplied by the price per unit.

The key point (break-even point) is the intersection of the total cost line and the total income line (Point P). A vertical line down from this point shows the level of production necessary to cover all costs. Production greater than this level generates positive revenue; losses are incurred at lower levels of production.

Mathematical Explanation

B-E = break-even point (units of production),

Example 1

A farmer wants to buy a new combine rather than hire a custom harvester. The total fixed costs for the desired combine are $21,270 per year. The variable costs (not counting the operator’s labor) are $8.75 per hour. The farmer can harvest 5 acres per hour. The custom harvester charges $16.00 per acre. How many acres must be harvested per year to break-even?

B-E = $21,270 / ($16/A — $1.75/A) = $21,270 / $14.25/A = 1,493 Acres

Example 2

Break-even analysis can be easily extended to consider other changes. If the farm operator can save two additional bushels of wheat per acre more than the custom harvester, what would be the break-even point if wheat is worth $4/bushel?

Additional income = $4/bu * 2 bu/A = $8/A

B-E = $21,270 / ($16/A + $8/A — $1.75/A)

= $21,270 / $22.25/A = 956 Acres

Example 3

A farmer raising 1,200 acres of wheat per year considers purchasing a combine. How much additional return (to land, capital labor, management and risk) would result?

Additional return = (savings or additional income) — (fixed costs + variable costs)

Additional profit = [ $16/ac + ($4/bu * 2 bu/ac) ] x 1200 A = $21,270 + [ ($8.75/hr / 5 A/hr) x 1200 A] = $28,800-$23,370 = $5,430

Thus, the farmer would generate another $5,430 in additional return by purchasing the combine. A farmer harvesting only 900 acres would probably choose not to buy the combine because the acreage is below the break-even point of 956 acres. The farmer may want to evaluate the purchase of a smaller or used combine.

Problem 1. If the fixed costs for the combine are $12,000 per year, no additional yield is expected, variable costs are $7 per hour and the farmer can combine 4 acres per hour, what is the new break-even point?

Problem 2. If 900 acres are harvested, what is the effect on the farmer’s profits?