Black Scholes and the normal distribution
Post on: 1 Июнь, 2015 No Comment
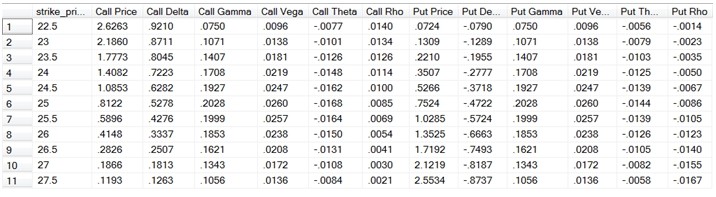
Black Scholes and the normal distribution
There have been lots of comments and confusion, especially in this post. over what people in finance do or do not assume about how the markets work. I wanted to dispel some myths (at the risk of creating more).
First, theres a big difference between quantitative trading and quantitative risk. And there may be a bunch of other categories that also exist, but Ive only worked in those two arenas.
Markets are not efficient
In quantitative trading, nobody really thinks that markets are efficient. Thats kind of ridiculous, since then what would be the point of trying to make money through trading? We essentially make money because they arent. But of course thats not to say they are entirely inefficient. Some approaches to removing inefficiency, and some markets, are easier than others. There can be entire markets that are so old and well-combed-over that the inefficiencies (that people have thought of) have been more or less removed and so, to make money, you have to be more thoughtful. A better way to say this is that the inefficiencies that are left are smaller than the transaction costs that would be required to remove them.
Its not clear where removing inefficiency ends and where a different kind of trading begins, by the way. In some sense all algorithmic trades that work for any amount of time can be thought of as removing inefficiency, but then it becomes a useless concept.
Also, you can see from the above that traders have a vested interest to introduce new kinds of markets to the system, because new markets have new inefficiencies that can be picked off.
This kind of trading is very specific to a certain kind of time horizon as well. Traders and their algorithms typically want to make money in the average year. If theres an inefficiency with a time horizon of 30 years it may still exist but few people are patient enough for it (I should add that we also probably dont have good enough evidence that theyd work, considering how quickly the markets change). Indeed the average quant shop is going in the opposite direction, of high speed trading, for that very reason, to find the time horizon at which there are still obvious inefficiencies.
Black-Scholes
A long long time ago, before Black Monday in 1987, people didnt know how to price options. Then Black-Scholes came out and traders started using the Black-Scholes (BS) formula and it worked pretty well, until Black Monday came along and people suddenly realized the assumptions in BS were ridiculous. Ever since then people have adjusted the BS formula. Everyone.
There are lots of ways to think about how to adjust the formula, but a very common one is through the volatility smile. This allows us to remove the BS assumption of constant volatility (of the underlying stock) and replace it with whatever inferred volatility is actually traded on in the market for that strike price and that maturity. As this commenter mentioned. the BS formula is still used here as a convenient reference to do this calculation. If you extend your consideration to any maturity and any strike price (for the same underlying stock or thingy) then you get a volatility surface by the same reasoning.
Two things to mention. First, you can think of the volatility smile/ surface as adjusting the assumption of constant volatility, but you can also ascribe to it an adjustment of the assumption of a normal distribution of the underlying stock. Theres really no way to extricate those two assumptions, but you can convince yourself of this by a thought experiment: if the volatility stays fixed but the presumed shape of the distribution of the stocks gets fatter-tailed, for example, then option prices (for options that are far from the current price) will change, which will in turn change the implied volatility according to the market (i.e. the smile will deepen). In other words, the smile adjusts for more than one assumption.
The other thing to mention: although weve done a relatively good job adjusting to market reality when pricing an option, when we apply our current risk measures like Value-at-Risk (VaR) to options, we still assume a normal distribution of risk factors (one of the risk factors, if we were pricing options, would be the implied volatility). So in other words, we might have a pretty good view of current prices, but its not at all clear we know how to make reasonable scenarios of future pricing shifts.
Ultimately, this assumption of normal distributions of risk factors in calculating VaR is actually pretty important in terms of our view of systemic risks. We do it out of computational convenience, by the way. That and because when we use fatter-tailed assumptions, people dont like the answer.














