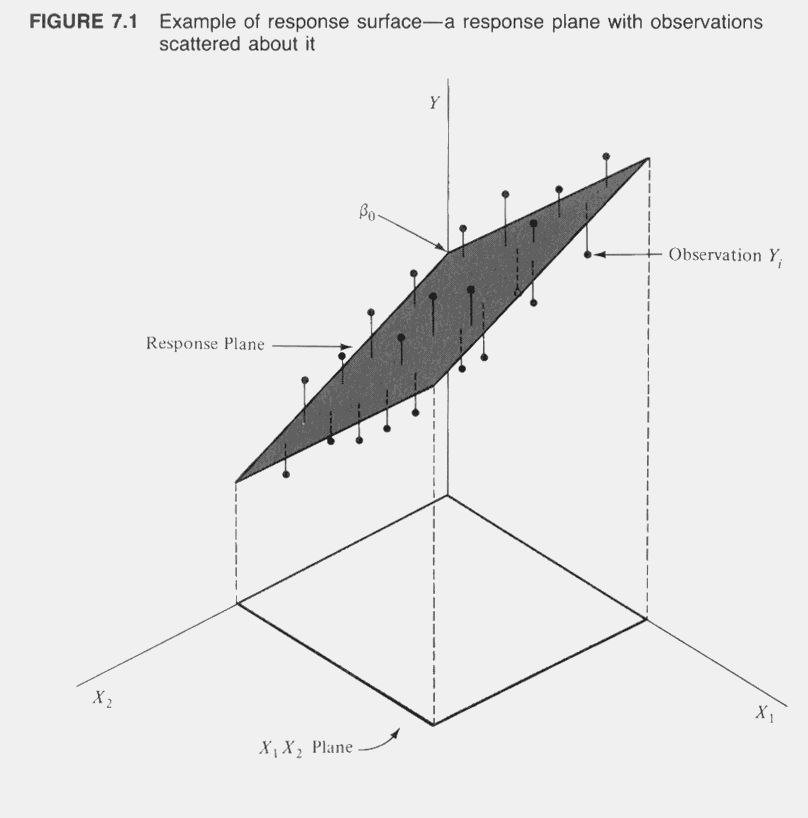
Multiple Regression
Post on: 27 Июль, 2015 No Comment
General Purpose
The general purpose of multiple regression (the term was first used by Pearson, 1908) is to learn more about the relationship between several independent or predictor variables and a dependent or criterion variable. For example, a real estate agent might record for each listing the size of the house (in square feet), the number of bedrooms, the average income in the respective neighborhood according to census data, and a subjective rating of appeal of the house. Once this information has been compiled for various houses it would be interesting to see whether and how these measures relate to the price for which a house is sold. For example, you might learn that the number of bedrooms is a better predictor of the price for which a house sells in a particular neighborhood than how pretty the house is (subjective rating). You may also detect outliers, that is, houses that should really sell for more, given their location and characteristics.
Personnel professionals customarily use multiple regression procedures to determine equitable compensation. You can determine a number of factors or dimensions such as amount of responsibility (Resp ) or number of people to supervise (No_Super ) that you believe to contribute to the value of a job. The personnel analyst then usually conducts a salary survey among comparable companies in the market, recording the salaries and respective characteristics (i.e. values on dimensions) for different positions. This information can be used in a multiple regression analysis to build a regression equation of the form:
Salary = .5*Resp + .8*No_Super
Once this so-called regression line has been determined, the analyst can now easily construct a graph of the expected (predicted) salaries and the actual salaries of job incumbents in his or her company. Thus, the analyst is able to determine which position is underpaid (below the regression line) or overpaid (above the regression line), or paid equitably.
In the social and natural sciences multiple regression procedures are very widely used in research. In general, multiple regression allows the researcher to ask (and hopefully answer) the general question what is the best predictor of. . For example, educational researchers might want to learn what are the best predictors of success in high-school. Psychologists may want to determine which personality variable best predicts social adjustment. Sociologists may want to find out which of the multiple social indicators best predict whether or not a new immigrant group will adapt and be absorbed into society.
Computational Approach
The general computational problem that needs to be solved in multiple regression analysis is to fit a straight line to a number of points.
Least Squares
In the scatterplot, we have an independent or X variable, and a dependent or Y variable. These variables may, for example, represent IQ (intelligence as measured by a test) and school achievement (grade point average; GPA), respectively. Each point in the plot represents one student, that is, the respective student’s IQ and GPA. The goal of linear regression procedures is to fit a line through the points. Specifically, the program will compute a line so that the squared deviations of the observed points from that line are minimized. Thus, this general procedure is sometimes also referred to as least squares estimation . 
The Regression Equation
A line in a two dimensional or two-variable space is defined by the equation Y=a+b*X ; in full text: the Y variable can be expressed in terms of a constant (a ) and a slope (b ) times the X variable. The constant is also referred to as the intercept. and the slope as the regression coefficient or B coefficient. For example, GPA may best be predicted as 1+.02*IQ. Thus, knowing that a student has an IQ of 130 would lead us to predict that her GPA would be 3.6 (since, 1+.02*130=3.6).
For example, the animation below shows a two dimensional regression equation plotted with three different confidence intervals (90%, 95% and 99%).
In the multivariate case, when there is more than one independent variable, the regression line cannot be visualized in the two dimensional space, but can be computed just as easily. For example, if in addition to IQ we had additional predictors of achievement (e.g. Motivation, Self- discipline ) we could construct a linear equation containing all those variables. In general then, multiple regression procedures will estimate a linear equation of the form:
Unique Prediction and Partial Correlation
Note that in this equation, the regression coefficients (or B coefficients) represent the independent contributions of each independent variable to the prediction of the dependent variable. Another way to express this fact is to say that, for example, variable X1 is correlated with the Y variable, after controlling for all other independent variables. This type of correlation is also referred to as a partial correlation (this term was first used by Yule, 1907). Perhaps the following example will clarify this issue. You would probably find a significant negative correlation between hair length and height in the population (i.e. short people have longer hair). At first this may seem odd; however, if we were to add the variable Gender into the multiple regression equation, this correlation would probably disappear. This is because women, on the average, have longer hair than men; they also are shorter on the average than men. Thus, after we remove this gender difference by entering Gender into the equation, the relationship between hair length and height disappears because hair length does not make any unique contribution to the prediction of height, above and beyond what it shares in the prediction with variable Gender. Put another way, after controlling for the variable Gender. the partial correlation between hair length and height is zero.
Predicted and Residual Scores
The regression line expresses the best prediction of the dependent variable (Y ), given the independent variables (X ). However, nature is rarely (if ever) perfectly predictable, and usually there is substantial variation of the observed points around the fitted regression line (as in the scatterplot shown earlier). The deviation of a particular point from the regression line (its predicted value) is called the residual value.
Residual Variance and R-square
R-Square. also known as the Coefficient of determination is a commonly used statistic to evaluate model fit. R-square is 1 minus the ratio of residual variability. When the variability of the residual values around the regression line relative to the overall variability is small, the predictions from the regression equation are good. For example, if there is no relationship between the X and Y variables, then the ratio of the residual variability of the Y variable to the original variance is equal to 1.0. Then R-square would be 0. If X and Y are perfectly related then there is no residual variance and the ratio of variance would be 0.0, making R-square = 1. In most cases, the ratio and R-square will fall somewhere between these extremes, that is, between 0.0 and 1.0. This ratio value is immediately interpretable in the following manner. If we have an R-square of 0.4 then we know that the variability of the Y values around the regression line is 1-0.4 times the original variance; in other words we have explained 40% of the original variability, and are left with 60% residual variability. Ideally, we would like to explain most if not all of the original variability. The R-square value is an indicator of how well the model fits the data (e.g. an R-square close to 1.0 indicates that we have accounted for almost all of the variability with the variables specified in the model).
Interpreting the Correlation Coefficient R
Customarily, the degree to which two or more predictors (independent or X variables) are related to the dependent (Y ) variable is expressed in the correlation coefficient R. which is the square root of R-square. In multiple regression, R can assume values between 0 and 1. To interpret the direction of the relationship between variables, look at the signs (plus or minus) of the regression or B coefficients. If a B coefficient is positive, then the relationship of this variable with the dependent variable is positive (e.g. the greater the IQ the better the grade point average); if the B coefficient is negative then the relationship is negative (e.g. the lower the class size the better the average test scores). Of course, if the B coefficient is equal to 0 then there is no relationship between the variables.














