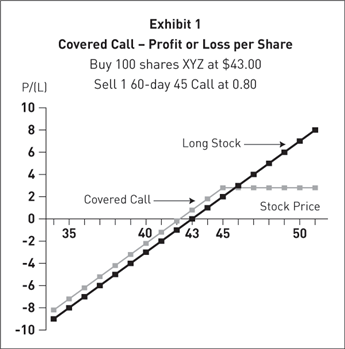
Call — Put = Stock — Strike

Put Call Parity is a theorem that defines a price relationship between a call option, put option and the underlying stock.

The conditions for the official theorem to hold true are;

• The options are of European style
• Identical strike price for both call and put options
• No brokerage or exchange fees (called a frictionless market)
• Interest rates remain constant until the expiration date
• The stock pays no dividends

In practice, however, the Put Call Parity relationship is used for many different asset types as a means of gauging an approximate value of a call or a put relative to its other components. The original formula provides the basis and we’ll take a look later in the article how to account for American style stock options that pay dividends.

Put Call Parity Formula

The basic version of the Put Call Parity formula is;

Call — Put = Stock — Strike

The formula supposes the existence of two portfolios that are of equal value at the expiration date of the options. The premise is that if the two portfolios have identical values at expiration then they must be worth the same value now. If one portfolio was worth more than the other then traders would buy the undervalued asset and sell the overvalued asset until no further opportunity exists — also referred to as the no arbitrage principle.

This therefore means that buying a call and put at the same strike price with the same expiration date will have the same value as the stock price minus the strike price. Given this, the payoff profile of each side will also be the same and we can see this with a synthetic long stock profile, which is long call and short put.

Put Call Parity Example

Let’s look at some real world examples of put call parity to understand how prices fit together.

Take a look at the option series below for MSFT.

As an example, let’s look at the $26 strike and see if the prices in the market prove put call parity. We’ll see if we can back out the price of the call option given the prices of the other components.

If we rearrange the put call parity equation to solve for the call option we have;

Call = Stock — Strike + Put

Entering in the values from the market;

Call = 26.04 — 26.00 + 1.80

Call = 1.84

Mmm. The last traded price of the call option in the market, however, is 1.66: a difference of 0.18. Why is this?

Well, as mentioned earlier, the basic formula we’ve used so far assumed European options on stocks that don’t pay dividends. But MSFT is a company that does pay dividends to its’ stock holders and the options traded are of American style. So how can we account for dividends with put call parity?

Put Call Parity with Dividends

As we know stocks pay dividends and these dividends affect the future valuation of the stock as money is being taken out of the company and paid to its’ shareholders. Because options have an expiration date, we need to value the option not against the current price of the stock but against what the expected value will be at the expiration date. This is known as the forward price.

Let’s take the basic put call parity formula Call — Put = Stock — Strike and expand on this to account for the underlying stocks’ dividends and interest rates. This makes the stock component Stock + Interest — Dividends. So now we have;

Call — Put = (Stock + Interest — Dividends) — Strike

And finally, as the strike price is the expected exercise price in the future we need to discount that value by the interest rates to a present value by dividing the strike by e ^ rt.

The complete formula will now read;

Call — Put = (Stock + Interest — Dividends) — PV(Strike)

Or, simplified;

Call — Put = FV(Stock) — PV(Strike)

Where FV = Future Value and PV = Present Value.

Now going back to our MSFT example, let’s apply dividends and interest rates and see if the market agrees with put call parity.

First, we need to check if MSFT is paying a dividend prior to the expiration of the options. For US stocks we can find this information easily on Yahoo under company events.

MSFT went ex-dividend on the 15th November for a payment of 0.20. Looking back we can see that the data shown on Yahoo confirms that the stock was adjusted on the 15th for a 0.20 dividend;

Next, we’ll add the dividend information into our put call parity equation assuming 0.25% interest rates (World Interest Rates Table ) and 94 days until the expiration date.

Call = FV(Stock) — PV(Strike) + Put

Where;

FV(Stock) = Stock + Interest — Dividends

FV(Stock) = 26.04 * (1.0025 ^ (94/365)) — 0.20

FV(Stock) = 25.85675

PV(Strike) = 26.00 / (1.0025 ^ (94/365))