Pricing Options Based on Trinomial Markov Tree

1 School of Economics and Management, Southeast University, Nanjing 210096, China

2 School of Economics and Management, Nanjing University of Information Science & Technology, Nanjing 210044, China

Received 14 March 2014; Revised 25 June 2014; Accepted 26 June 2014; Published 16 July 2014

Academic Editor: Beatrice Paternoster

Abstract

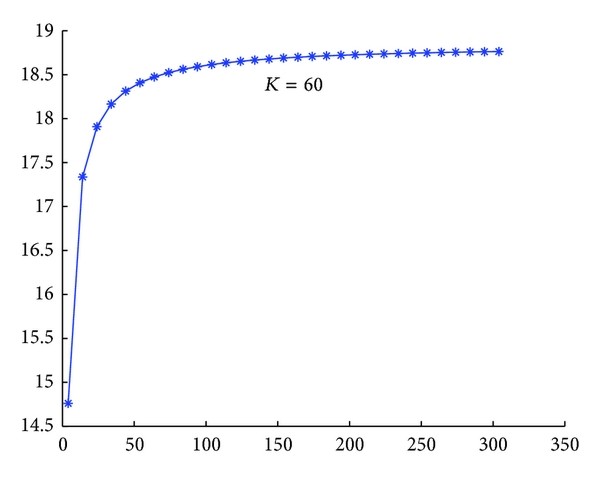
A trinomial Markov tree model is studied for pricing options in which the dynamics of the stock price are modeled by the first-order Markov process. Firstly, we construct a trinomial Markov tree with recombining nodes. Secondly, we give an algorithm for estimating the risk-neutral probability and provide the condition for the existence of a validation risk-neutral probability. Thirdly, we propose a method for estimating the volatilities. Lastly, we analyze the convergence and sensitivity of the pricing method implementing trinomial Markov tree. The result shows that, compared to binomial Markov tree, the proposed model is a natural combining tree and, while changing the probability of the node, it is still combining, so the computation is very fast and very easy to be implemented.

1. Introduction

Pricing options have attracted a lot of scholars to research about pricing option by use of tree methods. Black and Scholes put forward the famous pricing option model [1 ]. However, the knowledge of mathematics of this model is too deep and difficult to understand, and it is not widely known by the general readers. Merton published a paper titled “theory of rational option pricing” so as to achieve a major breakthrough in the field of pricing option for they developed the model known as “Black-Scholes” formula or “Black-Scholes-Merton” [2 ]. Later, Cox et al. proposed a binomial pricing option model that is widely understood and easy to accept due to its brief mathematical methods and the implicit economic importance, so it is widely used in financial markets [3 ]. However, because the model only allows two possible states: rise and fall when the underlying asset price changes at a certain time interval, which could lead to large errors in the numerical calculation, especially for the more complex options.

Boyle raised the Trinomial Pricing option Model [4 ] then Boyle, Boyle et al. Boyle and Lau, and Kamrad and Ritchen showed the modified trinomial pricing option model and its solution. They suppose that there are three variations states in the price of the underlying asset at a certain time interval, which is up, down, and equal. This is more realistic than the binomial model and makes trinomial tree model for pricing option more accurate in the solution and faster in convergence speed than the binary option, which makes it widely used in pricing more complex option models [5 –8 ]. Zhang solved the pricing option problem under the framework of the uncertain volatility model proposed by Avellaneda; Levy and Par. A trinomial tree can be used to solve the pricing problem for arithmetic average Asian option calculated based on the single stock model [9 ].

Han raised the trinomial tree model to price options for specific cases in numerical methods and drew relevant results: compared with the binomial model, the trinomial tree model can better approximate to the continuous distribution of the underlying asset price movements with more states and has higher accuracy [10 ].

Liu et al. assumed interest rates follows a Markov process and derived a different pricing option formula [11 ]. He compared the rate of convergence between trinomial tree model and binary tree model based on the number of nodes produced, computer time used, and the approximation error and provided the examples to explain that the accuracy of the trinomial tree model was better than that of the binary tree model through Visual Basic program [12 ].

Xiong presented a binomial pricing option model based on the MCMC method and concluded that it is more accurate than the usual binomial pricing option model although they both underestimate the option price of market [13 ]. An algorithm for pricing barrier options in one-dimensional Markov models is presented by Mijatović and Pistorius [14 ].

Xiong proposed a trinomial pricing option model based on Bayesian Markov Chain Monte Carlo Method which compared the classical binomial tree model, the classical trinomial tree model, the BS model, and the warrant price by using the actual data of the Chinese warrant market; the result shows that the price deviation of the trinomial tree pricing option model based on Bayesian MCMC method is smaller than any other models, although they all underestimate the market price [15 ].

Yuen and Yang put forward a fast and simple tree model to price simple and exotic options in Markov regime switching model (MRSM) with multiregime. They modified the trinomial tree model of Boyle [4 ] by controlling the risk neutral probability measure in different regime states to ensure that the tree model can accommodate the data of all different regimes and at the same time preserving its combining tree structure [16 ]. Bhat and Kumar (2012) proposed the Markov tree (MT) model for pricing option by a non-IID process, a modification of the standard binomial pricing options model, that takes this first-order Markov behavior into account [17 ]. Then pricing option under a normal mixture distribution derived from the Markov tree model is shown and concludes that the mixture of the two normal distributions fits much better than a single normal.

The existing studies on pricing option by tree methods mainly focus on binomial Markov tree or just trinomial but not considering the first-order Markov process. By construction, the trinomial model has advantage of simplified paths; on the other hand, the probability of the trinomial tree’s node is not unique. Hence, the trinomial Markov tree can be seen as combining the strengths of non-IID (independent and identically distributed) models, and trinomial tree methods all within the framework of risk-neutral pricing. In this paper, the main contribution is threefold. (1) A trinomial Markov tree for pricing American options with recombining nodes is proposed. (2) The condition for the existence of a validation risk-neutral probability is provided. (3) An algorithm for estimating the volatilities is given. The essential difference between the trinomial Markov tree and the traditional trinomial tree is that the next period stock price depends not only on the current stock price but also on the history stock price in the trinomial Markov tree model proposed, but the next period stock price only depends on the current stock price in the traditional trinomial tree model.

2. First-Order Markov Process

At first, introduce the definition of first-order Markov process. Set a sequence