Exercise Arbitrage

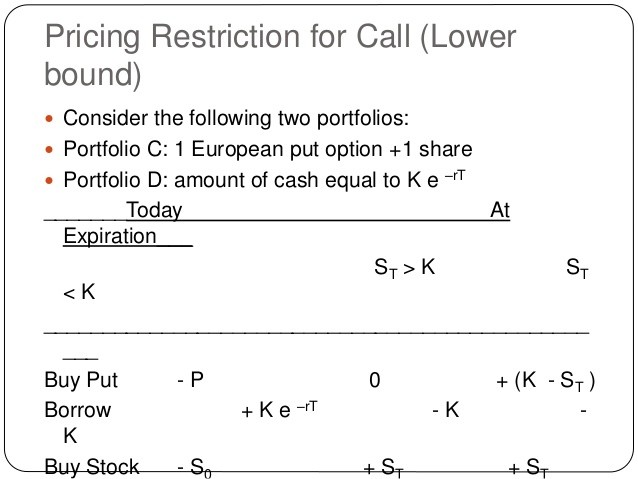
The easiest arbitrage opportunities in the option market exist when options violate simple pricing bounds. No option, for instance, should sell for less than its exercise value. With a call option: Value of call > Value of Underlying Asset � Strike Price

With a put option: Value of put > Strike Price � Value of Underlying Asset

For instance, a call option with a strike price of $ 30 on a stock that is currently trading at $ 40 should never sell for less than $ 10. It it did, you could make an immediate profit by buying the call for less than $ 10 and exercising right away to make $ 10.

In fact, you can tighten these bounds for call options, if you are willing to create a portfolio of the underlying asset and the option and hold it through the option�s expiration. The bounds then become:

With a call option: Value of call > Value of Underlying Asset � Present value of Strike Price

With a put option: Value of put > Present value of Strike Price � Value of Underlying Asset

Too see why, consider the call option in the previous example. Assume that you have one year to expiration and that the riskless interest rate is 10%.

Present value of Strike Price = $ 30/1.10 = $27.27

Lower Bound on call value = $ 40 — $27.27 = $12.73

The call has to trade for more than $12.73. What would happen if it traded for less, say $ 12? You would buy the call for $ 12, sell short a share of stock for $ 40 and invest the net proceeds of $ 28 ($40 � 12) at the riskless rate of 10%. Consider what happens a year from now:

If the stock price > 30: You first collect the proceeds from the riskless investment ($28(1.10) =$30.80), exercise the option (buy the share at $ 30) and cover your short sale. You will then get to keep the difference of $0.80.

If the stock price < 30: You collect the proceeds from the riskless investment ($30.80), but a share in the open market for the prevailing price then (which is less than $30) and keep the difference.

In other words, you invest nothing today and are guaranteed a positive payoff in the future. You could construct a similar example with puts.

The arbitrage bounds work best for non-dividend paying stocks and for options that can be exercised only at expiration (European options). Most options in the real world can be exercised only at expiration (American options) and are on stocks that pay dividends. Even with these options, though, you should not see short term options trading violating these bounds by large margins, partly because exercise is so rare even with listed American options and dividends tend to be small. As options become long term and dividends become larger and more uncertain, you may very well find options that violate these pricing bounds, but you may not be able to profit off them.

Replicating Portfolio

One of the key insights that Fischer Black and Myron Scholes had about options in the 1970s that revolutionized option pricing was that a portfolio composed of the underlying asset and the riskless asset could be constructed to have exactly the same cash flows as a call or put option. This portfolio is called the replicating portfolio. In fact, Black and Scholes used the arbitrage argument to derive their option pricing model by noting that since the replicating portfolio and the traded option had the same cash flows, they would have to sell at the same price.

To understand how replication works, let us consider a very simple model for stock prices where prices can jump to one of two points in each time period. This model, which is called a binomial model, allows us to model the replicating portfolio fairly easily. In the figure below, we have the binomial distribution of a stock, currently trading at $ 50 for the next two time periods. Note that in two time periods, this stock can be trading for as much as $ 100 or as little as $ 25. Assume that the objective is to value a call with a strike price of 50, which is expected to expire in two time periods: