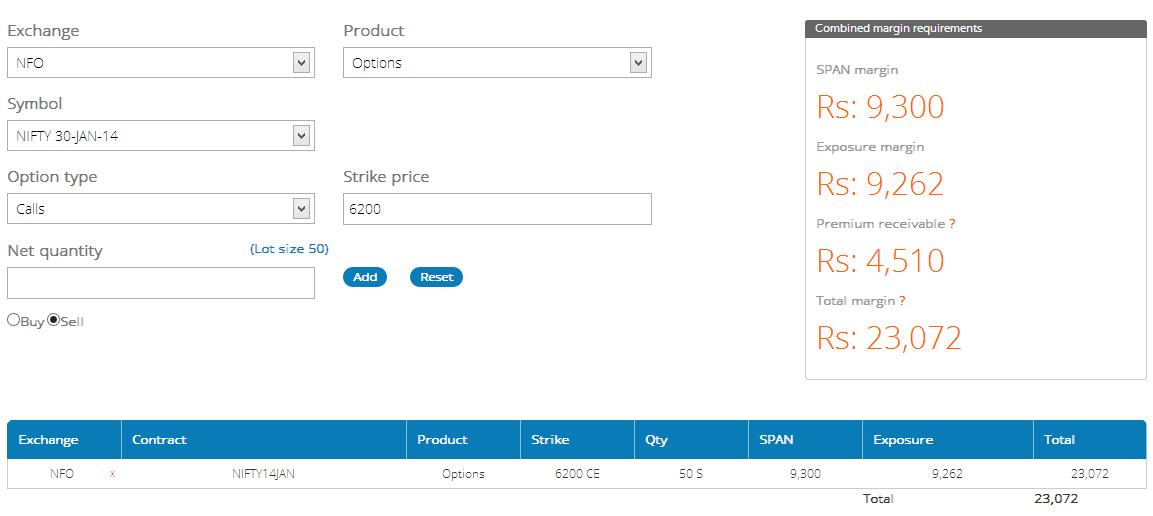
Dear users of the Options Calculator

Our Options Calculator evaluates the premium of index and equity options, for either American or European exercise style, with or without dividend.

All Exchange’s standard equity options are American style; whereas sponsored options on equity and indices are European style.

Valuing index and equity options

Select either index or equity options, then enter the following inputs:

the current level of the index or the current price of the stock underlying the option;

the strike price;

the volatility (you may use your own estimation, the value provided by your broker or the volatility link to calculate the implied volatility);

the annual interest rate: the risk-free interest rate usually measured by the annualized Treasury Bill rate for the period corresponding to the maturity of the option which you are evaluating, for instance, for a three-month option, use a 90-day rate;

for index options, the annual dividend yield which is available on the Toronto Stock Exchange Web site under Quote look-up or by contacting the TSE or Standard & Poors, which is the index supplier;

for equity options, the quarterly dividend amount and the next dividend date;

the expiration month or the days to expiration including all calendars days (including holidays);

for dividend paying stock options and American options, we use the numerical binomial model (Cox, Ross and Rubinstein, 1979). You can select the number of tree steps (between 2 and 60, the default is 30);

for all other options, we use the analytical model of Black and Scholes (1973).

Example:

How to price an American equity option maturing in 90 days with a strike price of $90, on a non-dividend paying stock, with a current price of $100, annual volatility of 20%, risk free annual rate of 5% on the 90-day period?

Select equity option, select American, and enter the following inputs:

Days to Expiry: 90

Underlying price: 100

Strike price: 90

Annual volatility (%): 20

Annual interest rate (%): 5

Quarterly Dividend ($): 0

Number of steps: 30

The theoretical call and put values will read respectively: 11.644 and 0.547.

Greek values, the standard measures of hedging sensitivity, are as important as computing the price of the option.

Delta tells you how much the option premium decreases when the stock or the index decreases by $1, keeping all other inputs constant. For example, when the stock price moves down from $100 to $99, the call premium decreases by $0.892 and the put premium increases by $0.11.

Gamma tells you how much the option delta decreases when the stock or the index decreases by $1, keeping all other inputs constant. For example, when the stock price moves down from $100 to $99, the option delta decreases by $0.019 for the put and the call.

Theta tells you how much the option premium decreases when the maturity decreases by 1 year, keeping all other inputs constant. For example, when the days to expiry decrease from 90 days to 80 days, the call premium decreases by 7.576 / 365 x 10 days = $0.20 and the put premium decreases by 3.312 / 365 x 10 days = $0.09.

Rho tells you how much the option premium decreases when the interest rate decreases by 1 percent, keeping all other inputs constant. For example, when the annual interest rate for the 90-day period moves down from 5% to 4%, the call premium decreases by $0.191 and the put premium increases by $0.025.

Vega tells you how much the option premium decreases when the annual volatility decreases by 1 percent, keeping all other inputs constant. For example, when the annual volatility moves down from 20% to 19%, the call premium decreases by $0.092 and the put premium decreases by $0.108.

Implicit volatility is computed by clicking on volatility. A dialog box prompts you to enter either the call or the put price. Using the previous example, if entering $12 as the call price, the implicit volatility is equal to 25%.