Research analysts use multivariate models to forecast investment outcomes to understand the possibilities surrounding their investment exposures and to better mitigate risks. Monte Carlo analysis is one specific multivariate modeling technique that allows researchers to run multiple trials and define all potential outcomes of an event or investment. Running a Monte Carlo model creates a probability distribution or risk assessment for a given investment or event under review. By comparing results against risk tolerances, managers can decide whether to proceed with certain investments or projects. (To learn more about Monte Carlo basics, see Introduction To Monte Carlo Simulation and Monte Carlo Simulation With GBM .)

Multivariate Models

Multivariate models can be thought of as complex, What if? scenarios. By changing the value of multiple variables, the modeler can ascertain his or her impact on the estimate being evaluated. These models are used by financial analysts to estimate cash flows and new product ideas. Portfolio managers and financial advisors use these models to determine the impact of investments on portfolio performance and risk. Insurance companies use these models to estimate the potential for claims and to price policies. Some of the best-known multivariate models are those used to value stock options. Multivariate models also help analysts determine the true drivers of value.

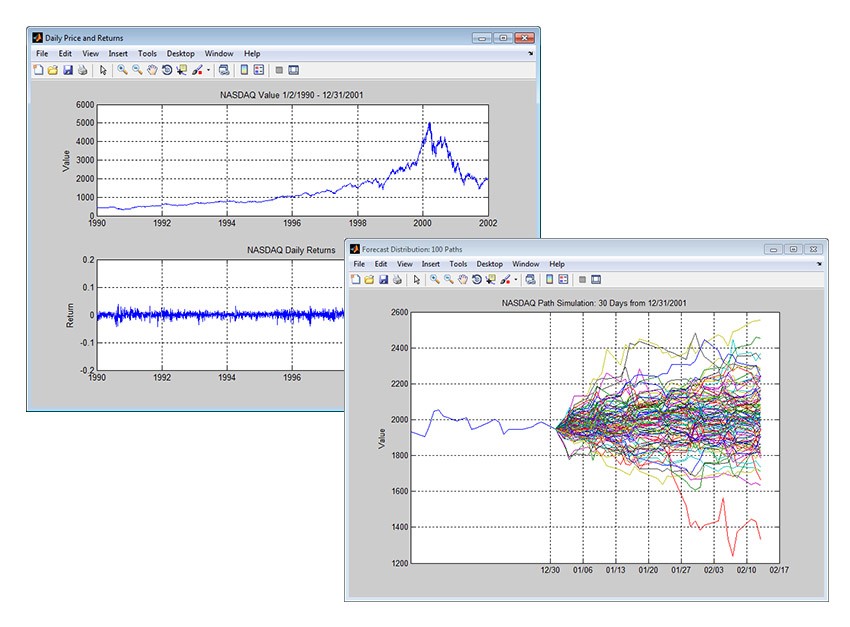
Monte Carlo Analysis

Monte Carlo analysis is named after the principality made famous by its casinos. With games of chance, all the possible outcomes and probabilities are known, but with most investments the set of future outcomes is unknown. It is up to the analyst to determine the set of outcomes and the probability that they will occur. In Monte Carlo modeling, the analyst runs multiple trials (often thousands) to determine all the possible outcomes and the probability that they will take place.

Monte Carlo analysis is useful for analysts because many investment and business decisions are made on the basis of one outcome. In other words, many analysts derive one possible scenario and then compare it to return hurdles to decide whether to proceed. Most pro forma estimates start with a base case. By inputting the highest probability assumption for each factor, an analyst can actually derive the highest probability outcome. However, making any decisions on the basis of a base case is problematic, and creating a forecast with only one outcome is insufficient because it says nothing about any other possible values that could occur. It also says nothing about the very real chance that the actual future value will be something other than the base case prediction. It is impossible to hedge or insure against a negative occurrence if the drivers and probabilities of these events are not calculated in advance. (To learn more about how to manage the risk in your portfolio, see our Risk and Diversification tutorial.)

Creating the Model

Once designed, executing a Monte Carlo model requires a tool that will randomly select factor values that are bound by certain predetermined conditions. By running a number of trials with variables constrained by their own independent probability of occurrence, an analyst creates a distribution that includes all the possible outcomes and the probability that they will occur. There are many random number generators in the marketplace. The two most common tools for designing and executing Monte Carlo models are @Risk and Crystal Ball. Both of these can be used as add-ins for spreadsheets and allow random sampling to be incorporated into established spreadsheet models.

The art in developing an appropriate Monte Carlo model is to determine the correct constraints for each variable and the correct relationship between variables. For example, because portfolio diversification is based on the correlation between assets, any model developed to create expected portfolio values must include the correlation between investments. (To learn more, read The Importance of Diversification .)

In order to choose the correct distribution for a variable, one must understand each of the possible distributions available. For example, the most common one is a normal distribution. also known as a bell curve. In a normal distribution, all the occurrences are equally distributed (symmetrical) around the mean. The mean is the most probable event. Natural phenomena, people’s heights and inflation are some examples of inputs that are normally distributed.