Sharpe (Ratio) Thinking about the Investment Opportunity Set and CAPM Relationship

Faculty of Economics, University of Agder, Service Box 422, 4604 Kristiansand, Norway

Received 6 December 2010; Revised 20 April 2011; Accepted 4 May 2011

Academic Editor: Yi-Ming Wei

Abstract

In the presence of a risk-free asset the investment opportunity set obtained via the Markowitz portfolio optimization procedure is usually characterized in terms of the vector of excess returns on individual risky assets and the variance-covariance matrix. We show that the investment opportunity set can alternatively be characterized in terms of the vector of Sharpe ratios of individual risky assets and the correlation matrix. This implies that the changes in the characteristics of individual risky assets that preserve the Sharpe ratios and the correlation matrix do not change the investment opportunity set. The alternative characterization makes it simple to perform a comparative static analysis that provides an answer to the question of what happens with the investment opportunity set when we change the risk-return characteristics of individual risky assets. We demonstrate the advantages of using the alternative characterization of the investment opportunity set in the investment practice. The Sharpe ratio thinking also motivates reconsidering the CAPM relationship and adjusting Jensen’s alpha in order to properly measure abnormal portfolio performance.

1. Introduction

The mean-variance model of asset choice has been proposed by Markowitz [1 ] and used extensively in finance principally due to a strong intuitive appeal and the existence of closed-form solutions to the optimal portfolio choice and equilibrium problems. The papers by Merton [2 ] and Roll [3 ] are the two seminal papers where the authors provide a rigorous characterization of the investment opportunity set in the absence and in the presence of a risk-free asset.

In the absence of a risk-free asset the investment opportunity set is characterized by the vector of expected returns on risky assets and the variance-covariance matrix. In the presence of a risk-free asset the investment opportunity set is characterized by the vector of excess returns on risky assets and the variance-covariance matrix. To demonstrate the classical characterization of the investment opportunity set one typically employs a two-dimensional standard deviation-expected return space. Next one illustrates the construction of the minimum-variance frontier of risky assets. In the absence of a risk-free asset the efficient part of the minimum-variance frontier of risky assets coincides with the investment opportunity set. In the presence of a risk-free asset one draws a straight line (whose intercept and slope are equal to the risk-free rate of return and the maximum Sharpe ratio, resp.) which is tangent to the efficient frontier of risky assets.

In this paper we show that in the presence of a risk-free asset the investment opportunity set can alternatively be characterized in terms of the vector of the Sharpe ratios of risky assets and the correlation matrix. This implies that the changes in the characteristics of individual risky assets that preserve the Sharpe ratios of risky assets and the correlation matrix do not change the investment opportunity set. In other words, two apparently different sets comprised of the same number of risky assets (different in terms of the values of expected returns and standard deviations), that produce apparently different minimum-variance frontiers of risky assets, will generate exactly the same investment opportunity set if the risky assets in the two sets have the same Sharpe ratios and correlation matrix.

The alternative characterization of the investment opportunity set in the presence of a risk-free asset implies that the two-dimensional standard deviation-expected return space, although instructive in teaching, can be redundant and misleading in practice. A more straightforward depiction of the characteristics of individual risky assets and the investment opportunity set can be done in one-dimensional Sharpe ratio space. For the case of two risky assets the alternative characterization allows to visualize the maximum Sharpe ratio as a function of the correlation coefficient.

In addition, the alternative characterization of the investment opportunity set provides a simple answer to the question of what happens with the investment opportunity set when we change the risk-return characteristics of individual risky assets. In other words, if we change the values of the expected returns and standard deviations of individual risky assets, will it result in an improvement or worsening of the investment opportunity set? Using the classical characterization of the investment opportunity set, the answer is not clear. With the alternative characterization of the investment opportunity set by means of the Sharpe ratios of individual risky assets, the answer is rather trivial. We show that if the weight of a risky asset in the optimal risky portfolio is positive, then an increase in the Sharpe ratio of this asset results in an improvement of the investment opportunity set. Moreover, if the market is in equilibrium, then an increase in the Sharpe ratio of any risky asset results in an increase in the maximum Sharpe ratio.

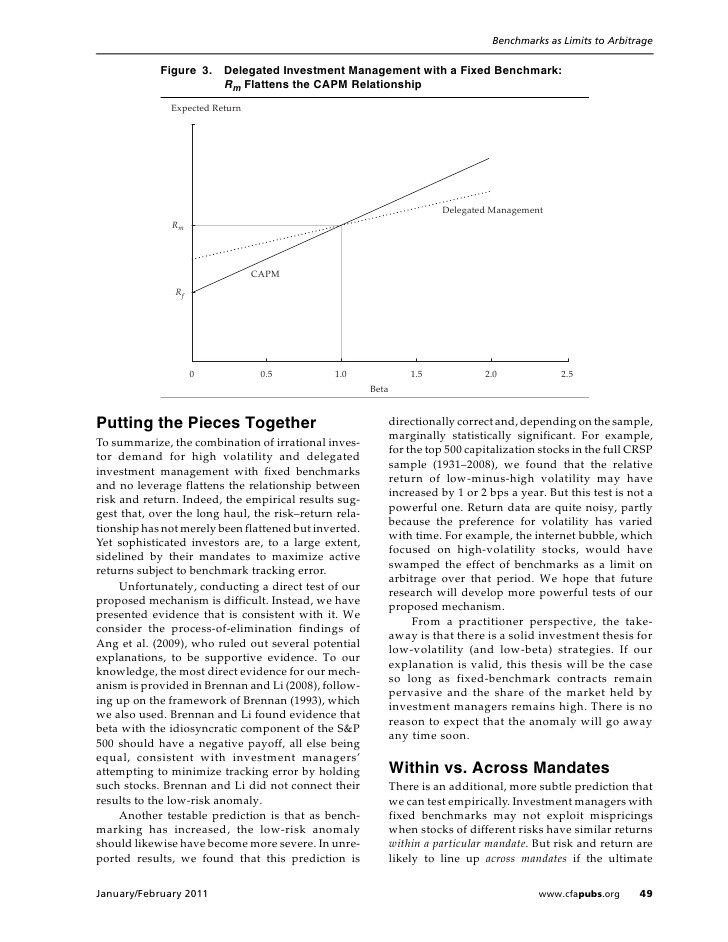
Finally, the alternative characterization of the investment opportunity set has a clear appeal to the investment practice. In particular, it is well known that the risk-return characteristics of individual risky assets and the correlations among them are changing over time. Existing academic studies usually address only the changing nature of correlations and try to deduce how these changes affect the investment opportunity set. The alternative characterization of the investment opportunity set motivates the idea that one also needs to examine the changing nature of the Sharpe ratios, in addition to that of the correlation structure, in order to have a full picture of the evolution of the investment opportunity set.

The classical CAPM is, in fact, none other than the Markowitz portfolio theory in the presence of a risk-free asset combined with an equilibrium condition. Therefore, the Sharpe ratio thinking motivates reconsidering the CAPM relationship in terms of Sharpe ratios. We show that the classical expected return-beta relationship can alternatively be represented by a Sharpe ratio-rho relationship (rho denotes the correlation coefficient between the returns on a risky asset and the market portfolio). Moreover, the Sharpe ratio thinking motivates adjusting Jensen’s alpha in order to properly measure abnormal portfolio performance. Instead of Jensen’s alpha we propose to use Jensen’s alpha divided by the total risk. In this manner the adjusted Jensen’s alpha becomes a true reward-to-risk performance measure that cannot be manipulated by leverage.

The rest of the paper is organized as follows. In Section 2 we review the classical characterization of the investment opportunity set in the presence of a risk-free asset. In Section 3 we derive the alternative characterization of the investment opportunity set and perform a comparative static analysis. In this section we also present several theoretical examples and one real-world example that illustrate the derived relationships and demonstrate the advantages of the alternative characterization of the investment opportunity set. In Section 4 we reconsider the CAPM relationship and introduce an adjusted Jensen’s alpha. Section 5 summarizes the paper.

2. The Maximum Sharpe Ratio

The purpose of this section is to introduce the notation, the investor’s optimal portfolio choice problem, and to derive the expression for the maximum Sharpe ratio that characterizes the investment opportunity set in the presence of a risk-free asset. We do not provide all details of the derivation because there are no new results in this section. Our exposition in this section is similar to that in Huang and Litzenberger [4. Chapter  3].

We suppose that the investment universe consists of