15 772

Technical trading can only be exploited if good tools are avaliable.

The tools of a good trader are experience, judgement, and a mathematical hierarchy provided by good trading computer program.

Introduction

The first part of the article Indicators and Trade Systems in MQL5 by William Blau. Part 1: Indicators is a description of indicators and oscillators, described by William Blau in the book Momentum, Direction, and Divergence .

The indicators and oscillators, described in this article, are presented as a source codes in MQL5 language and attached in the archive file Blau_Indicators_MQL5_en.zip.

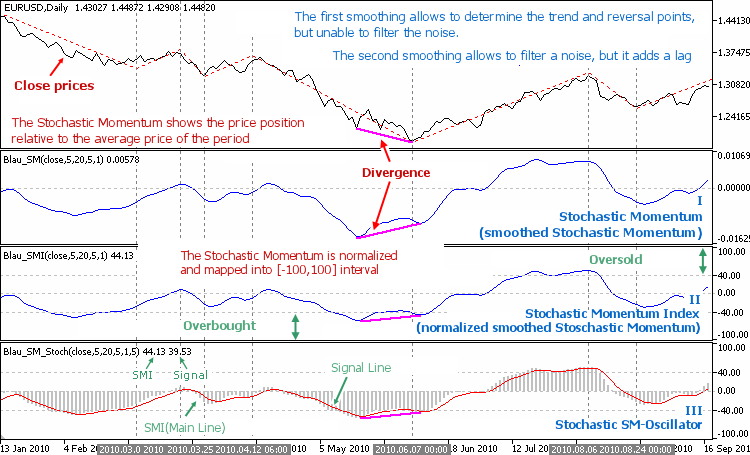
1. Using the price series data (q bars) the indicator is calculated and plotted at chart. The indicator does not reflect the general trend of the price movement, and does not allow to determine the trend reversal points.
2. The indicator is smoothed several times using the EMA method: the first time (with period r), the second time (with period s), and the third time (with period u); a smoothed indicator is plotted. A smoothed indicator fairly accurately and reproduces the price fluctuations with a minimum lag. It allows to determine the trend of the price movement and the reversal points and eliminates the price noise.
3. The smoothed indicator is normalized, a normalized smoothed indicator is plotted. The normalization allows the indicator value to be interpreted as the overbought or oversold states of the market.
4. A normalized smoothed indicator is smoothed once by the EMA method (period ul); an oscillator is constructed — the indicator histogram and the signal line, the levels of overbought and oversold of the market are added. Oscillator allows us to distinguish the overbought/oversold states of the market, the reveral points and the end of a trend.

Indicators

The article describes the following groups of indicators:

1. Indicators, based on the Momentum:

• Stochastic (Blau_TStoch.mq5)
• Stochastics Index (Blau_TStochI.mq5)
• Stochastic Oscillator (Blau_TS_Stochastic.mq5)

The True Strength Index section contains:

• A detailed analysis of William Blau’s approach in the aspect of the technical analysis of the price chart;
• A detailed description of the algorithm and code of each indicator of the Momentum-based indicators groups.

As a smoothing method William Blau uses the exponentially smoothed Moving Average s (EMA). The Exponential Moving Average is calculated by adding to the previous value of the Moving Average, a certain percentage of the current price.

When using the EMA, the latest prices have a greater weight.

The function of calculating of EMA:

where:

• EMA(k,n) — exponentially smoothed moving average of period n for the moment of period k;
• price(k) — the price at the moment of period k.

The description of the four types of moving averages and the methods of their use in technical analysis (see also iMA ) can be found in the MetaTrader 5 Help (Analytics/Technical Indicators/Trend Indicators/ Moving Average ).

The Library of Functions

The library of functions for calculating the moving averages is located in the MovingAverages.mqh. We are concerned with the ExponentialMAOnBuffer(), which fills the output array buffer[] with EMA values of the input array price[]. However, the implementation of the ExponentialMAOnBuffer() presented in the MovingAverages.mqh has the disadvantage that it does not work with the period n = 1.

See in the source code:

However, William Blau in his book uses the smoothing period n = 1 as the absence of smoothing.

Therefore, the code of the ExponentialMAOnBuffer() function has undergone a few changes:

and we obtain the ExponentialMAOnBufferWB(). The code of this function is located in the file WilliamBlau.mqh.

The file WilliamBlau.mqh also has the following the functions:

• The PriceName() function returns the price type as a string:

• The CalculatePriceBuffer() function calculates the price array of this price type:

The applied price type and the timeframe of the price chart

William Blau considers the closing prices of the Daily timeframe. The indicators, developed in this article, allow you to choose the price type (see price constants ) the timeframe of the price chart depends on the timeframe of the indicator (see chart timeframes ).

1. The True Strength Index

The considered indicators (see attachment):

1. Blau_Mtm.mq5 — Indicator of the rate (q-period Momentum; smoothed q-period Momentum);
2. Blau_TSI.mq5 — True strengths Index (Normalized smoothed q-period Momentum);
3. Blau_Ergodic.mq5 — Ergodic Oscillator (based on the True Strength Index).

1.1. Momentum

The description of the built-in technical indicator Momentum. and its use is in technical analysis can be found in the MetaTrader 5 Help section Analytics/Technical Indicators/Oscillators/Momentum (see also iMomentum ). In contrast to the standard Momentum (iMomentum ) the Momentum by William Blau calculates the Momentum as the absolute price change.

An example of the MQL5-implementation of the True Strength Indicator (TSI) by William Blau is presented in the article MQL5: Create Your Own Indicator .

1.1.1. Technical analysis using Momentum indicator

The object of the technical analysis is the price chart of the financial instrument. Each element of the chart is a price bar. The price bar has the following characteristics: opening time. opening price. maximum price. minimum price. closing price. trading volumes. and other. The price bar is formed and reflects the behavior of prices during a specific discrete time period (chart timeframe ).

The task of the technical analysis of the price chart is to determine the current trend of the price movement, reveal the price peaks and bottoms and predict the direction of the price change in the coming period of time. The complexity of this, is that the price, while moving within the limits of its basic tendency, makes multi-directional fluctuations creating a so-called price-noise.

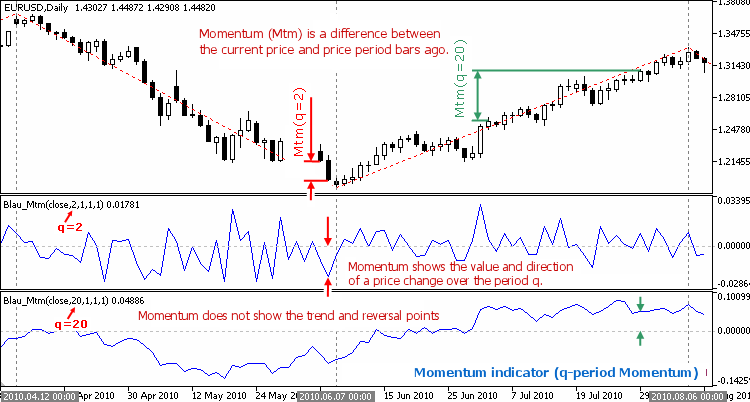
What William Blau has proposed. The first difference: the Momentum. William Blau calculated the Momentum as a relative to the price change [closing] for every [day] period of time; and created the Momentum indicator. From a mathematical point of view the Momentum function is the first derivative of the price.

Fig. 1.1. Momentum Indicator (q-period Momentum)

The Momentum displays one-day period price fluctuations shows the speed (magnitude) and the direction of the price changes over this period, but it does not reflect the general trend of the price movement, and does not determine the trend reversal points.

The second difference is the smoothing. The moving average of the Momentum (the cumulative sum of daily price fluctuations) almost exactly reproduces both, the major and local variations of the curve prices. Fig. 1.2 (a) in the subwindows I, II present the smoothed Momentum (moving averages with periods 20 and 300, respectively).

The higher is the period of the Moving Average, the more accurately the smoothed Momentum approximates (reproduces) the fluctuations of the price curve. From a mathematical point of view the function of smoothening the Momentum is the integral function of the momentum, or the restored function of the price.

Fig. 1.2 (a). Momentum Indicator (smoothed q-period Momentum)

Fig. 1.2 (b). Momentum Indicator (smoothed q-period Momentum)

In Fig. 1.2 (a), in the main window, the EMA-smoothed (with periods of 5, 20, 100) indicators are presented. A slight increase in the period of the moving average leads to a lag and the moving average practically becomes unable to reproduce the fluctuations of the price curve.

The third difference is the resmoothing. The first smoothing of the Momentum defines the main trend of the price movement, as well as the reversal points, but does not eliminate the noise. To eliminate the price noise a re-smoothing is needed with a small period of the moving average.

Fig. 1.2 (b), in the sub-window I presents the smoothed Momentum indicator (moving average with period 20), the subwindows II and III present the double-and triple-smoothed Momentum (periods of moving average of 5, 3). A repeated smoothing eliminates the price noise, but adds a slight shift of the curve (a lag).

The fourth difference: the difference in a signal of changing trends. The smoothing of Momentum with a small averaging period may lead to a divergence of the smoothed Momentum with the trend of the price curve.

On Fig. 1.2 (a), the discrepancy is observed in the subwindow I, and on Fig. 1.2 (b) — in the subwindows I, II, III (the direction of the price changes diverges from the direction of the change in the smoothed Momentum). Such differences often indicates a trend change. From a mathematical point of view the divergence is a function of the smoothing period.

The reliability of the interpretation of these differences as a signal of changing trends can be improved if we consider the divergence only for the overbought or oversold areas (see п. 1.2.1).

1.1.2. Definition of the Momentum

The Momentum is a relative price change.

The sign of the Momentum shows the direction of the price change: a positive Momentum — the price increased over the period, a negative — the price has declined over the period. The magnitude of the Momentum — is the relative speed of the price change (first derivative of the price).

Fig. 1.3. Definition of the Momentum

Formula of the Momentum :

where:

• price — price [closing] of the current period;
• price [1] — price of [closing] of the previous period.

William Blau examines the momentum as the difference of the price of [closing] of the current period and the price of [closing] of the previous period. William Blau, in his calculation of a single period momentum, uses the prices of two periods (the current and the previous periods).

We introduce into the formula for calculating the momentum a period indicator, q — is the number of time periods involved in the calculation (By William Blau q = 2).

Formula of q-period Momentum :

where:

• q — number of bars, used in the calculation of the momentum;
• price — price [closing] of the current period;
• price [q-1] — price of [closing] (q-1) periods ago.

In the resulting formula, our two period Momentum corresponds to one period relative Momentum of William Blau.

Formula of a smoothed q-period Momentum :

where:

• price — price of [closing] — the price base of the price chart;
• q — number of bars, used in calculation of the Momentum;
• mtm(price,q)=price-price[q-1] — q-period Momentum;
• EMA (mtm (price, q), r) — the first smoothing — the EMA(r), applied to the q-period Momentum;
• EMA (EMA(. r),s) — the second smoothing — the EMA(s), applied to the result of the 1st smoothing;
• EMA (EMA (EMA (. r), s), u) — the third smoothing — the EMA(u), applied to the result of the 2nd smoothing.

1.1.3. Mtm(price,q,r,s,u) — rate indicator (momentum). Specification

• File name. Blau_Mtm.mq5
• The name. Momentum (q-period Momentum; smoothed q-period Momentum) by William Blau.
• Input parameters :

• q — the period for which the Momentum is calculated (default q = 2);
• r -period of the 1-st EMA, applied to the Momentum (default r = 20);
• s — period of the 2nd EMA, applied to the result of the 1st smoothing (by default s = 5);
• u — period of the 3rd EMA, applied to the result of the 2nd smoothing (by default, u = 3);
• AppliedPrice — price type (default AppliedPrice= PRICE_CLOSE ).

1.2. The True Strengths Index

1.2.1. Technical analysis using the True Strength Index

Continued . See the beginning in Section 1.1.1.

The fifth: normalization. Bringing through the normalization of values of the smoothed Momentum to a single scale (mapping to the interval [-1, +1]), allows us to determine the overbought or oversold states of the market. Repeated multiplication of the values ​​of the normalized smoothed momentum a factor of 100 converts the numerical series in the percentage range (mapping to the interval [-100, 100]).

Fig. 1.4. Normalized Smoothed Momentum

A discrepancy as a signal of changing trends can be considered reliable if the normalized smoothed momentum is in the state of an overbought or oversold.

1.2.2. The definition of the True Strength Index

The True Strength Index (True Strength Index, TSI) — is an indicator of the normalized Momentum (normalized q-period Momentum). Bringing the values of the ​​smoothed Momentum to a single scale (mapping to the interval [-1, +1]) is provided with the normalization of each value of the smoothed Momentum (the cumulative sum of the smoothed q-period price fluctuations) by the value of the smoothed Momentum, taken in absolute value.

Multiplication by a coefficient of 100 changes the interval of the display to [-100, +100] (percent). Normalization allows the interpretation of the TSI value as a level of overbought (positive) or oversold (negative) market.

The formula of the True Strength Index :

where:

• price — price of [closing] — the price base of the price chart;
• q — period of the Momentum;
• mtm(price,q)=price-price[q-1] — q-period momentum;
• | Mtm (price, q) | — the absolute value of the q-period Momentum;
• Mtm (price, q, r, s, u) — three times smoothed q-period Momentum;
• EMA (. r) — the first smoothing — the EMA of period r, applied to:

1) q-period Momentum;

2) absolute value of the q-period Momentum;

1.2.3. TSI(price,q,r,s,u) — the True Strength Index. Specification

• File name. Blau_TSI.mq5
• The name. The True Strength Index (normalized smoothed q-period relative Momentum) by William Blau.
• Input parameters :

• q — the period for which the momentum is calculated (default q = 2);
• r -period of the 1-st EMA, applied to the Momentum (default r = 20);
• s — period of the 2nd EMA, applied to the result of the 1st smoothing (by default s = 5);
• u — period of the 3rd EMA, applied to the result of the 2nd smoothing (by default, u = 3);
• AppliedPrice — price type (default AppliedPrice= PRICE_CLOSE ).

1.3. Ergodic oscillator

1.3.1. Technical analysis using the Ergodic Oscillator

Continued . See the beginning in Secs. 1.1.1, 1.2.1.

Sixth: the areas of an overbought and oversold market. Unit interval [-1, +1] or a percentage interval [-100.100], within which changes occur in the values ​​of the normalized smoothed momentum, allows you to define the areas overbought or oversold market.

The class of indexes of technical analysis, which characterize the state of overbought or oversold market, is called the oscillator. For each oscillator, levels are determined, at the approach to which, the signals of an overbought or oversold market are received. Oscillators are ineffective on trending markets, as the market can be in an overbought/oversold conditions for an arbitrarily long period.

Seventh: The Signal Line. To obtain a signal about the end of a trend and a reversal trend of a price movement, a signal line is used. The signal to buy is received when the main line crosses the signal line from the bottom up. The signal to sell is received when the main line crosses the signal line from the top down. In the case where there is a main line — this is an ergodic (true strength index), then a re-smoothing of the ergodic forms a signal line. The re-smoothing procedure is equal to the last process of ergodic smoothing.

Eighth: the trend of the price movement. The trend of the price movement is upwards (upward trend), when the main line (ergodic) passes above the signal line. The trend of the price movement is downwards (downward trend), when the main line (ergodic) passes under the signal line.

Fig. 1.5. Ergodic Oscillator

1.3.2. Definition of the Ergodic Oscillator

where:

• Ergodic() — ergodic — True Strength Index TSI(price,q,r,s,u);
• The SignalLine() -a signal line — the EMA(ul), applied to the ergodic;
• ul — an EMA period of a signal line — according to William Blau, the ul value must be equal to the period of the last significant (>1) of the EMA ergodic. For example, if you are using a double smoothing Ergodic (price, q, r, s, u) = Ergodic (price, 2,20,5,1), then by William Blau ul = s = 5.

1.3.3. Ergodic (price, q,r,s,u,ul) — ergodic oscillator. Specification

• File name. Blau_Ergodic.mq5
• Name. Ergodic Oscillator (based on a true strength index) by William Blau.
• Input parameters :

• graphic plot #0 — Ergodic (a true strength index):

• q — the period for which the momentum is calculated (default q = 2);
• r -period of the 1-st EMA, applied to the Momentum (default r = 20);
• s — period of the 2nd EMA, applied to the result of the 1st smoothing (by default s = 5);
• u — period of the 3rd EMA, applied to the result of the 2nd smoothing (by default, u = 3);

1.4. The Code (detailed description)

1.4.1. Blau_Mtm.mq5 — indicator Mtm(price,q,r,s,u) — momentum