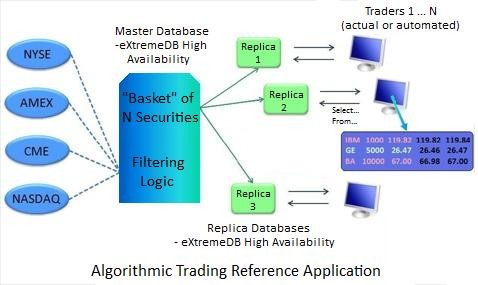
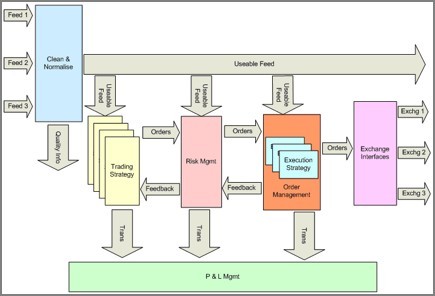
Trading Algorithms Data
Post on: 23 Май, 2015 No Comment
Genetic Algorithm to find and Optimize trading models and rules
Abstract
Trading models or rules are algorithms proposing trading recommendations for financial assets. In our approach we limit this definition to a set of rules based on past financial data Pictet et al.,(1992). The financial data, which are typically series of prices, enter the trading model in the form of indicators corresponding to various kinds of averages Brock et al.,(1992).Although progress has been made in understanding financial markets Muller et al. (1993) Guillaume et al. (1994), there is no definitive prescription on how to build a successful trading model and how to define the indicators. Automatic search and optimization techniques can be considered when addressing this problem. In this paper we explain how the relevant quantities of our application can be encoded in genes so as to fit the requirements of the genetic evolutionary optimization technique and new rules are created that are able to identify periods to be in the index when daily returns are positive and volatility is low and out when the reverse is true.
Keywords: Trading rules, Genetic algorithms, Genetic Programming.
1. Introduction
There are two trends or types of analysis used by stock market traders. Exponents of Fundamental Analysis start from the hypothesis that the market mirrors a company’s value based on its growth potential. They therefore anchor their forecasts on analysis of company accounts and trading figure projections. In this way, they can deduce whether a company is overvalued or under valued. Technical Analysis is the second of the two trends. Its advocates do not concern themselves with ‘fundamental’ values such as sales, regulations or the working environment, but instead base their ideas on the hypothesis that any factor that truly influences the market will immediately show up in a company’s share price and its negotiated volume. These technique therefore only studies indexes (digital filters Fama (1960) for share prices and negotiated volume) and the charts that describe their movements. Chart analysis is a part of Technical Analysis called Chartism.
The Stock Market has attracted considerable academic attention, given the enormous sums of capital that are moved around it, and the wide range of techniques applied to forecasting stock prices range from those that border on the philosophic, such as the Golden Proportions of Elliot Waves, to more elaborate techniques such as Fuzzy Logic and Chaos Theory. All of them pursue the same end to find some structure in a seemingly random signal. Another that is frequently used for the Stock market are indicators, which are generally based on weighted arithmetic averages, though these are little more than digital filters Fama (1960) applied to quotation prices and shares volume. Artificial Intelligence, particularly Genetic Algorithms Goldberg (1989) has opened new horizons in the field of stock market-focused fore casting. The first step in system design is to decide the approach to the problem. The following needs to be known: If you are out of the market, should you get into it? If you are in the market, should you get out?
Genetic algorithms belong to a class of machine learning algorithms that have been successfully used in a number of research areas. There is a growing interest. in their use in financial economics but so far there has been little formal analysis. The purpose of this paper is to demonstrate how they can be used to find technical trading rules. The techniques can be easily extended to include other types of information such as fundamental and macro-economic data as well as past prices.
Over the years there has been a large literature on the effectiveness of various technical trading rules. The majority of this literature has found that such rules do not make money. For instance, Alexander (1961) tests a number of filter rules, which advise a trader to buy if the price rises by a fixed percentage (5%, say) and sell if the price declines by the same percentage. Although such rules appear to yield returns above the buy-and-hold strategy for various stock indices, Alexander (1964) concludes that if transaction costs are adjusted, the filter rules are not profitable. These conclusions are supported by the results of Fama and Blume (1966), who find no evidence of profitable filter rules for the 30 Dow Jones stocks. On the whole, the studies during the 1960s provide little evidence of profitable trading rules, and lead Fama (1970) to dismiss technical analysis as a futile undertaking.
In a more recent study, Brock et al. (1992) consider the performance of various simple moving average rules in the absence of transaction costs. They find that these rules identify periods to be in the market (long the Dow Jones index) when returns are high and volatility is low and vice versa. All of this previous literature uses ad hoc specifications of trading rules. This leads to a problem of data snooping whereby the ex post specification of rules can lead to biased test results. We show how genetic algorithms can be used to derive trading rules that are not ad hoc but are in a sense optimal. Section 2 describes genetic algorithms. Section 3 shows how the rules are found and evaluated, and addresses the robustness of the results. Section 4 contains concluding remarks.
2. Genetic algorithms
2.1. Introduction to evolutionary algorithms
Genetic algorithms constitute a class of search, adaptation, and optimization techniques based on the principles of natural evolution. Genetic algorithms were developed by Holland (1962, 1975). Other evolutionary algorithms include evolution strategies Rechenberg, (1973),revolutionary programming Fogel et al. (1966), classifier systems Holland, (1976, 1980), and genetic programming Koza (1992). An evolutionary algorithm maintains a population of solution candidates and evaluates the quality of each solution candidate according to a problem-specific fitness function, which defines the environment for the evolution. New solution candidates are created by selecting relatively fit members of the population and recombining them through various operators. Specific evolutionary algorithms differ in the representation of solutions, the selection mechanism, and the details of the recombination operators.
In a genetic algorithm, solution candidates are represented as character strings from a given (often binary) alphabet. In a particular problem, a mapping between these genetic structures and the original solution space has to be developed, and a fitness function has to be defined. The fitness function measures the quality of the solution corresponding to a genetic structure. In an optimization problem, the fitness function simply computes the value of the objective function. In other problems, fitness could be determined by a evolutionary environment consisting of other genetic structures. For instance, one could study the equilibrium properties of game-theoretic problems whereby a population of strategies evolves with the fitness of each strategy defined as the average payoff against the other members of the population.
A genetic algorithm starts with a population of randomly generated solution candidates. The next generation is created by recombining promising candidates. The recombination involves two parents chosen at random from the population, with the selection probabilities biased in favor of the relatively fit candidates. The parents are recombined through a crossover operator, which splits the two genetic structures apart at randomly chosen locations, and joins a piece from each parent to create an offspring (as a safeguard against the loss of genetic diversity, random mutations are occasionally introduced into the offspring). The algorithm evaluates the fitness of the offspring and replaces one of the relatively unfit members of the population. New genetic structures are produced until the generation is completed. Successive generations are created in the same manner until a well-defined termination criterion is satisfied. The final population provides a collection of solution candidates, one or more of which can be applied to the original problem.
The theoretical foundation of genetic algorithms is laid out in Holland (1975). Maintaining a population of solution candidates makes the search process parallel, allowing an efficient exploration of the solution space. In addition to this explicit parallelism, genetic algorithms are implicitly parallel in that the evaluation of the fitness of a specific genetic structure yields information about the quality of a very large number of schemata, or building blocks. The so-called schema theorem shows that a genetic algorithm automatically allocates an exponentially increasing number of trials to the best observed schemata. This leads to a favorable tradeoff between exploitation of promising directions of the search space and exploration of less-frequented regions of the space. However, there is no general result guaranteeing the convergence of a genetic algorithm to the global optimum.
Evolutionary algorithms offer a number of advantages over more traditional optimization methods. They can be applied to problems with a non differentiable or discontinuous objective function, to which gradient-based methods such as Gauss- Newton would not be applicable. They are also useful when the objective function has several local optima. Because of the stochastic nature of the selection and recombination operators, evolutionary algorithms are less likely to converge to local maxima than hill-climbing or gradient-type methods. Evolutionary optimization methods can often be successfully applied when the size of the search space poses difficulties for other optimizations methods. In such problems, the parallel trial-and-error process is an efficient way to reduce the uncertainty about the search space.
Evolutionary algorithms do have limitations. Maintaining a population of genetic structures leads to an increase in execution time, due to the number of times the objective function must be evaluated. Since evolutionary algorithms embody very little problem-specific knowledge, they are unlikely to perform better and can be less efficient than special-purpose algorithms in well-understood domains. Despite the schema theorem, the lack of a theoretical convergence result is a weakness. In differentiable problems, an evolutionary algorithm may indeed converge to a point where the gradient is nonzero. This can happen if there is not enough genetic variation left in the population by the time the algorithm approaches the optimum. However, this last drawback can often be avoided by switching to hill-climbing when the genetic algorithm makes no further progress.
One should not view genetic algorithms or other members of the family as a replacement for other optimization methods. It is more productive to regard them as a complement, the usefulness of which depends on the nature of the problem. Even though evolutionary algorithms are not guaranteed to find the global optimum, they can find an acceptable solution relatively quickly in a wide range of problems.
Evolutionary algorithms have been applied to a large number of problems in engineering, computer science, cognitive science, economics, management science, and other fields (for references, see Goldberg, 1989; Booker et al. 1989). The number of practical applications has been rising steadily, especially since the late 1980s. Typical business applications involve production planning, job-shop scheduling, and other difficult combinatorial problems. Genetic algorithms have also been applied to theoretical questions in economic markets, to time series forecasting, and to econometric estimation (see, e.g. Marimon et al.,1990; Dorsey and Mayer, 1995). String-based genetic algorithms have been applied to finding market-timing strategies based on fundamental data for stock and bond markets by Bauer (1994).
2.2. Genetic programming
In traditional genetic algorithms, genetic structures are represented as character strings of fixed length. This representation is adequate for many problems, but it is restrictive when the size or the form of the solution cannot be assessed beforehand. Genetic programming, developed by Koza (1992), is an extension of genetic algorithms that partly alleviates the restrictions of the fixed-length representation of genetic structures. For the purposes of this paper, the main advantage of genetic programming is the ability to represent different trading rules in a natural way.
In genetic programming, solution candidates are represented as hierarchical compositions of functions. In these tree-like structures, the successors of each node provide the arguments for the function identified with the node. The terminal nodes (i.e. nodes with no successors) correspond to the input data. The entire tree is also interpreted as a function, which is evaluated recursively by simply evaluating the root node of the tree. The structure of the solution candidates is not specified a priori. Instead, a set of functions is defined as building blocks to be recombined by the genetic algorithm.
The function set is chosen in a way appropriate to the particular problem under study. Koza focuses much of his work on genetic structures that include only functions of a single type. However, genetic programming possesses no inherent limitations about the types of functions, as long as a so-called closure property is satisfied. This property holds if all possible combinations of sub trees result in syntactically valid composite functions. Closure is needed to ensure that the recombination operator is well defined.
Genetic programming also maintains a population of genetic structures. The initial population consists of random trees. The root node of a tree is chosen at random among functions of the same type as the desired composite function. Each argument of that function is then selected among the functions of the appropriate type, proceeding recursively down the tree until a function with no arguments (a terminal node) is reached. The evolution takes place much as in the basic genetic algorithms, selecting relatively fit solution candidates to be recombined and replacing unfit individuals with the off spring.
In genetic programming, the crossover operator recombines two solution candidates by replacing a randomly selected sub tree in the first parent with a sub tree from the second parent. If different types of functions are used within a tree, the appropriate procedure involves choosing the crossover node at random within the first parent, and then choosing the crossover node within the second parent among the nodes of the same type as the crossover node in the first tree. Mutations are introduced by using a randomly generated tree in place of the second parent with a small probability.
3. The Genetic Algorithms Application
3.1Finding and evaluating trading rules
Most of the previous trading rule studies have sought to test whether particular kinds of technical rules have forecasting ability. A machine learning approach to finding testable trading rules sheds light on a question that is subtly different. Instead of asking whether speci fic rules work, we seek to find out whether in a certain sense optimal rules can be used to forecast future returns. Allowing a genetic algorithm to compose the trading rules avoids much of the arbitrariness involved in choosing which rules to test. Were we to use a more traditional search method, we would have to decide the form of the trading rules before searching through the parameter space for the chosen class of rules. By using a genetic algorithm, we can look for both the structure and the parameters of the rules at the same time.
The rules found by the genetic algorithm are optimal in a very specific sense. The algorithm finds rules that maximize one particular though intuitive measure of fitness. In addition, some structure must be imposed on the rule space. One issue that needs to be addressed in the design of the genetic algorithm is the possibility of over fitting the training data. The task of inferring technical trading rules relies on the assumption that there are some underlying regularities in the data. However, there are going to be patterns arising from noise, and the trick is to find trading rules that generalize beyond the training sample. The problem is common to all methods of non-linear statistical inference, and several approaches have been proposed to avoid over fitting. These include reserving a part of the data as a validation set on which to test the predictions, increasing the amount of training data, penalizing for model complexity, and minimizing the amount of information needed to describe both the model and the data (for a discussion of over fitting, see Gershenfeld and Weigend, 1993). We reserve a selection period immediately following the training period for validation of the inferred trading rules. After each generation, we apply the fittest rule (based on the excess return in the training period) to the selection period. If the excess return in the selection period improves upon the best previously saved rule, the new rule is saved.
To minimize over fitting during optimization, the optimization process must include the following important ingredients:
A good measure of the trading model performance (Pictet et al. 1992),
Indicator evaluation for different time series,
Large data samples,
A robust optimization technique,
Last but not least, strict testing procedures.
3.2 Applying genetic programming to finding trading rules
The goal of the algorithm is to find decision rules that divide days into two distinct categories, either in the market (earning the market rate of return) or out of the market (earning the risk-free rate of return). Each genetic structure represents a particular technical trading rule. A trading rule is a function that returns either a buy or a sell signal for any given price history. The trading strategy specifies the position to be taken the following day, given the current position and the trading rule signal. The trading strategy is implemented as a simple automaton, which works as follows: If the current state is in (i.e. holding the market) and the trading rule signals sell, switch to out (move out of the market); if the current state is out and the trading rule signals buy, switch back to in. In the other two cases, the current state is preserved.
Building blocks for trading rules include simple functions of past price data, numerical and logical constants, and logical functions that allow the combination of low-level building blocks to create more complicated expressions. The root node of each genetic structure corresponds to a Boolean function. This restriction ensures that the trading strategy is well defined.
The function set includes two kinds of functions: real and Boolean. The real-valued functions include a function that computes a moving average of past prices (average) in a time window. There are also functions that return the local extrema of prices (maximum and minimum) during a time window of a given length. Other real-valued functions include arithmetic operators (+, -, %, * ) and a function returning the absolute value of the difference between two real numbers (norm). Boolean functions include logical functions (if-then-else, and, or, not) and comparisons of two real numbers (>, <). In addition, there are Boolean constants (true, false) and real constants.
The functions defined above can be used to implement many commonly used technical trading rules. For instance, Fig. 1 shows a 50-day moving average rule on the left and a simple 30-day trading range break rule on the right. The moving average rule asks whether the moving average of closing prices over the past 50 days is less than today’s closing price and if so returns a buy (stay in) signal and a sell (stay out) signal otherwise. The 30-day trading range break rule is evaluated in the same way, asking whether today’s closing price is above the maximum closing price during the last 30 days.
Fig. 2 depicts how the genetic algorithm combines simple rules to create more complicated ones (a crossover). The two trading rules shown in the top of Fig. 2 are used as the parents. In the first parent, the crossover node chosen at random corresponds to the Boolean sub tree designated by the dotted line. In the second parent, the crossover node is selected at random among nodes of the Boolean type. Replacing the sub tree in the first parent with the sub tree of the second parent generates the trading rule shown in the bottom of Fig. 2. This new rule returns a buy signal if both the moving average rule and the trading range break rule are satisfied and a sell signal otherwise. Proceeding in the same way, complex and delicate nonlinear rules can be created, although nothing prevent the discovery of quite elementary decision rules.
3.3 Applying genetic algorithm to finding trading rules
To start with, an initial population of rules is created at random. The algorithm determines the fitness of each trading rule by applying it to the daily data in the training period. It then creates a new generation of rules by recombining parts of relatively fit rules in the population. After each generation, the best rule in the population is applied to a selection period. If the rule leads to a higher excess return than the best rule so far, the new rule is saved. The evolution terminates when there is no improvement in the selection period for a predetermined number of generations, or when a maximum number of generations is reached. The best rule is then applied to the out-of-sample test period immediately following the selection period. If no rule better than the buy-and-hold strategy in the training period emerges in the maximum number of generations, the trial is abandoned.
Table 1
One trial of the genetic algorithm used to find technical trading rules
Step 1
Create a random rule.
Compute the fitness of the rule as the excess return in the training period above the buy-and-hold strategy.
Do this 500 times (this is the initial population).
Step 2
Apply the fittest rule in the population to the selection period and compute the excess return. Save this rule as the initial best rule.
Step 3
Pick two parent rules at random, using a probability distribution skewed towards the best rule. Create a new rule by breaking the parents apart randomly and recombining the pieces (this is a crossover).
Compute the fitness of the rule as the excess return in the training period above the buy-and-hold strategy.
Replace one of the old rules by the new rule, using a probability distribution skewed towards the worst rule.
Do this 500 times (this is called one generation).
Step 4
Apply the fittest rule in the population to the selection period and compute the excess return. If the excess return improves upon the previous best rule, save as the new best rule. Stop if there is no improvement for 25 generations or after a total of 50 generations. Otherwise, go back to Step 3.
3.4 Fitness Measure
The fitness measure is based on the excess return over the buy-and-hold strategy. The fitness of a rule is computed as the excess return over the buy-and-hold strategy during a training period. To evaluate the fitness of a trading rule, it is applied to each trading day to divide the days into periods in (earning the market return) or out of the market (earning a risk-free return). The continuously compounded return is then computed, and the buy-and-hold return and the transaction costs are subtracted to determine the fitness of the rule. The simple return from a single trade (buy at date bi i . sell at si i ) is thus
where P t is the closing price (or level of the composite stock index) on day t ,
r t = log P t - log P t -1 is the daily continuously compounded return, and c denotes the one-way transaction cost (expressed as a fraction of the price). Let t be the number of trading days and let r f (t ) denote the risk-free rate on day t. Define two indicator variables, I b(t ) and I s (t ), equal to one if a rule signals buy and sell, respectively, and zero otherwise with the indicator variables satisfying the relation I b(t ) * I s (t )= 0 t
Lastly, let n denote the number of trades, i.e. the number of buy signals followed by a subsequent sell signal (an open position in the last day is forcibly closed). Then, the continuously compounded return for a trading rule can be computed as
T T
t =1 t =1
The return for the buy-and-hold strategy (buy the first day, sell the last day) is
t =1
and the excess return or fitness for a trading rule is given by
3.5 Characterizing the trading rules
There are a number of interesting questions regarding the nature of the rules found by the genetic algorithm. This section describes what the rules look like and analyzes what kind of price behavior triggers the trading rule signals. The structure and complexity of the rules found by the algorithm vary across different trials. While many of the rules appear to be quite complicated at first sight, there is often a lot of redundant material in the form of duplicated sub trees. If some of these sub trees are never visited when the rules are evaluated, seemingly complex tree structures can be effectively similar to much simpler ones. Consequently, measuring the complexity of the trading rules cannot in general be done by inspection of the tree structures.
As an example of what the trading rules look like the tree structure shown in Fig. 3 can be reduced to the expression Price*minimum(price)-0.0688*price>0.8943. This is roughly equivalent to a rule that takes a position in the market when normalized prices are above 0.89 and is out of the market otherwise.
4. Conclusions
This article formulates an approach to the issue of stock market speculation from the perspective of when to buy in. Decisions are taken according to the values of certain technical rules, with a Genetic Algorithm finding the optimum investment. We use a genetic algorithm to learn technical trading rules rather than having them exogenously specified as in previous studies.
There is an important question of why there appears to be systematic relation between trading rule signals and volatility. One hypothesis is that the trading rule results can be explained by investors reactions to changes in the expected volatility. In most equilibrium models, expected excess returns are positively related to risk as measured by the expected volatility of the market. When volatility is lower (higher) than expected, expected returns decrease (increase), and the corresponding upward (downward) revision of prices is picked up by the trading rules. Given the negative excess returns after trading costs and the lack of ability to forecast returns with delayed signals, markets process the information about the expected volatility in an efficient way.
This paper studies a base case in which a genetic algorithm is applied to a broad stock index, and finds evidence of economically significant technical trading rules. Rules learned by evolutionary algorithms could also be tested on liquid markets with low transaction costs, including financial futures, commodities, and foreign exchange markets. One could also develop the methodology further. The genetic algorithm we use is a relatively simple one, and the parameters are not necessarily optimal. More importantly, the current algorithm uses very limited information for its inputs. It would be interesting to apply a similar technique to learn fundamental trading rules by changing the building blocks to include the desired fundamental variables.
References
Alexander, S.S. 1961. Price movements in speculative markets: trends or random walks. Industrial Management Review 2, 7- 26.
Bauer, R.J. Jr. 1994. Genetic Algorithms and Investment Strategies. Wiley, New York.
Booker, L.B. Goldberg, D.E. Holland, J.H. 1989. Classifier systems and genetic algorithms.ArtiÞcial Intelligence 40, 235-282.
Brock, W. Lakonishok, J. LeBaron, B. 1992. Simple technical trading rules and the stochastic properties of stock returns. Journal of Finance 47, 1731-1764.
Dorsey, R.E. Mayer, W.J. 1995. Genetic algorithms for estimation problems with multiple optimal non differentiability, and other irregular features. Journal of Business and Economic Statistics 13, 53-66.
Fama, E.F. Blume, M.E. 1966. Filter rules and stock market trading. Security prices: a supplement.Journal of Business 39, 226-241.
Gershenfeld, N.A. Weigend, A.S. 1993. The future of time series: learning and understanding. In:Weigend, A.S. Gershenfeld, N.A. (Eds.), Time Series Prediction: Forecasting the Future and Understanding the Past, Santa Fe Institute Studies in the Sciences of Complexity, Proceedings vol. XV. Addison- Wesley, Reading, pp. 1- 70.
Koza, J.R. 1992. Genetic Programming: On the Programming of Computers by Means of Natural Selection. MIT Press, Cambridge.
Marimon, R. McGrattan, E. Sargent, T.J. 1990. Money as a medium of exchange in an economy with artiÞcially intelligent agents. Journal of Economic Dynamics and Control 14, 329- 373.
Merton, R.C. 1980. On estimating the expected return on the market: an exploratory investigation.
Neftci, S.N. 1991. Naive trading rules in Þnancial markets and Wiener-Kolmogorov prediction theory: a study of technical analysis. Journal of Business 64, 540-571.
Schwefel, H.-P. 1981. Numerical Optimization of Computer Models. Wiley, New York.
Vose, M.D. 1991. Generalizing the notion of a schema in genetic algorithms. Artificial Intelligence 50, 385- 396.
Pictet O. V. Dacorogna M. M. Muller U. A. Olsen R. B. and Ward J. R. 1992,
Real-time trading models for foreign exchange rates, Neural Network World, 2(6), 713-744.














