Arbitrage

Arbitrage means the ability to earn a profit without risk.  One method by which arbitrage is commonly accomplished by buying an asset in one market, and simultaneously selling an identical asset in another market at a higher price (e.g. T-Notes or T-Bonds).  Another is by borrowing an asset (e.g. a currency) and investing it at a guaranteed return that is higher than the borrowing cost.  A third is by trading one asset for an identical asset (e.g. ETFs, multi-currency trades, put-call parity).

Arbitrageurs are essential to fair pricing in financial markets, because they ensure that returns on (economically) identical transactions are equal.  Because of the presence of arbitrageurs in financial markets, the pricing of many securities (e.g. futures, forwards, swaps, FRAs, coupon-paying bonds, options, etc.) is based on the presumption of no arbitrage: the price is determined so that no arbitrage opportunity is available.

Ill present a few arbitrage transactions to show you how no-arbitrage pricing works in theory on a few types of securities; you can then extrapolate those ideas to the pricing of other types of securities.  At the end, Ill describe the difference between arbitrage in theory and arbitrage in practice.

Treasury Notes and Treasury Bonds

T-Notes and T-Bonds comprise a series of cash flows.  For example, a 10-year, 6% coupon T-Note has 21 cash flows: 20 coupon payments – $30 payable six months from today, $30 payable one year from today, and so on – and one principle payment: $1,000 payable 10 years from today.  These bonds can be stripped – broken apart into 21 separate securities – and the components sold as separate, zero-coupon bonds: a 6-month, $30 zero, a one-year, $30 zero, an 18-month, $30 zero. a 10-year, $30 zero, and a 10-year, $1,000 zero.  Conversely, a complete set of these 21 strips can be reconstituted into a T-Note and sold as a single, coupon-paying bond.

The no-arbitrage condition for these bonds, then, is that the price of the bond has to equal the sum of the prices of the individual strips.  If the bond were priced higher than the sum of the strip prices, the arbitrage transaction would be to purchase the strips and simultaneously sell the bond, making a profit without risk.  If the price of the bond were lower than the sum of the strip prices, the arbitrage transaction would be to purchase the bond and simultaneously sell the strips, making a profit without risk.

This no-arbitrage conditions manifests itself in the relationship between the Treasury spot curve and the Treasury par curve.  The spot curve is used to price zero coupon bonds, and the par curve is used to price coupon-paying bonds.  If the discount rates arent compatible, an arbitrage opportunity will arise.  The method for deriving the spot rates from the par rates is called bootstrapping, and is described in the article on the par curve, spot curve, and forward curve .  Therefore, only a brief example will be given here.

Suppose that we have the following (BEY) spot rates:

6-month: 1.5% 1-year: 1.8% 18-month: 2.0% 2-year: 2.1%

Using these spot rates, the price of a 2-year, semiannual pay, 6% coupon, $1,000 par bond would be:

&= $29.78 + $29.47 + $29.12 + $987.85\

\&= $1,076.21

Therefore, the YTM (BEY par rate) for this bond has to satisfy:

Solving this for YTM gives:

[YTM = 2.0893%]

If the YTM were anything other than 2.0893%, there would be an arbitrage opportunity.

Currency Forward Exchange Rates

The no-arbitrage condition for forward exchange rates on currencies is that you have to earn the same risk-free return investing in currency A as you would if you engaged in the following series of transactions:

1. Convert currency A to currency B at the spot rate
2. Invest currency B at its risk-free rate
3. Convert currency B back to currency A at the forward rate

A full treatment of this is covered in the article on interest rate parity .  Therefore, only a brief example will be given here.

Suppose that you are given the following information about the CAD and the GBP:

• The spot rate is CAD/GBP 1.7791 (i.e. CAD1.7791 = GBP1.00)

• The 1-year risk-free GBP rate is 2%
• The 1-year risk-free CAD rate is 2.4%

If you invest GBP1,000 for one year, risk-free, you will end up with GBP1,020.  Thus, if you:

• Exchange GBP1,000 for CAD1,779.10 today
• Invest CAD1,779.10 for one year at 2.4%, ending with CAD1,821.80 (= CAD1,779.10 × 1.024)
• Convert CAD1,821.80 to GBP

you must also end up with GBP1,020.  So, the one-year forward exchange rate must be:

[frac = CAD/GBP 1.7861]

If the one-year forward rate were anything other than CAD/GBP 1.7861, there would be an arbitrage opportunity.

Multi-Currency Spot Exchange Rates

The no-arbitrage condition for multi-currency exchange rates is that if you start with currency A and end with currency B, you should get the same exchange rate whether you exchange A for B directly, or whether you go through one or more intermediate currencies along the way.  A full treatment of this is presented in the article on currency exchange rates .  Therefore, only a brief example will be given here.

Suppose that you are given the following spot exchange rates:

• CAD/GBP 1.7791 (i.e. CAD1.7791 = GBP1.00)
• EUR/CAD 0.6737 (i.e. EUR0.6737 = CAD1.00)

If you exchange GBP1,000 for CAD, you will receive CAD1,779.10 (= 1,000 × 1.7791).  If you exchange CAD1,779.10 for EUR, you will receive EUR1,198.58 (= 1,779.10 × 0.6737).  Therefore, if you exchange GBP1,000 directly for EUR, you must receive the same amount: EUR1,198.58; so the EUR/GBP spot rate must be 1.19858 (= 1,198.58 ÷ 1,000).  This can be written as:

If the EUR/GBP spot rate were anything other than 1.19858, there would be an arbitrage opportunity.

This idea can be extended to more currencies: if you exchange GBP1,000 for CAD, then CAD for JPY, then JPY for AUD, then AUD for EUR, you must still end up with EUR1,198.58.

ETFs

The no-arbitrage condition for ETFs is known as in-kind creation and redemption . an investor can trade a portfolio of securities held by the ETF (in the same proportions as the portfolio) for an equivalent number of shares of the ETF, and can redeem shares of the ETF for an equivalent portfolio of securities held by the ETF.  This feature of ETFs ensures that their share prices are always very close to their NAV.

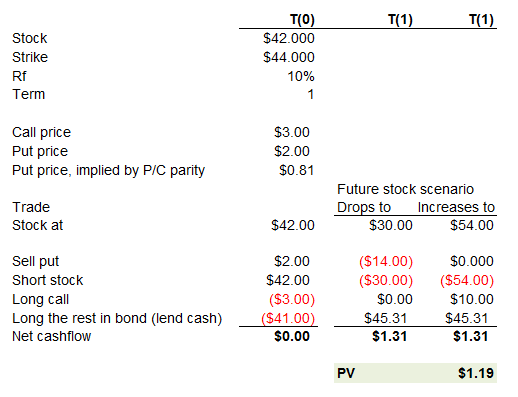
Put-Call Parity

The no-arbitrage condition for put options and call options is that because a protective put and a fiduciary call (same underlying, same strike price, same expiry) have the same payoff under all circumstances, they have to have the same price.  A full treatment is presented in the article on put-call parity .  Therefore, only the put-call parity equation is presented here:

[S_0 + p_0 = c_0 + frac<left(1 + r_right)^t>]

Abuse of the Term Arbitrage

You should be aware that finance people love to take terms with narrow, concrete definitions and expand their use to similar situations to which the strict definitions would not apply.  So it is with arbitrage.  The term is commonly used in situations in which profits are not earned risk-free.  Sometimes it is applied to sets of transactions that are not simultaneous, so that there is some risk that not all of the transactions will occur, or will not generate the profit originally envisioned.  At other times it is applied to situations involving similar – but not identical – securities.  Thus, you may hear of merger arbitrage (buying the stock of the target company and selling the stock of the acquiring company), convertible bond arbitrage (buying a convertible bond, selling a nonconvertible bond, and buying credit insurance), and so on.

Arbitrage in Practice

All of the arbitrage conditions described above give an exact value for a particular quantity: an exact YTM for a bond, an exact forward currency exchange rate, an exact currency spot rate, or an exact ETF share price.  What the theoretical conditions have omitted – for simplicity – are transaction costs.  When transaction costs are included, the arbitrage conditions will not give an exact value for each quantity.  In practice, the arbitrage conditions will generally give a range of values between which no arbitrage profit is possible (because the profit would not exceed the transaction costs); if the value lies outside the range (e.g. if the YTM is either less than 2.08% or greater than 2.10%), then there would be an arbitrage opportunity because the arbitrage profit will exceed the transaction costs.