Traditional decision analysis methods can provide an intuitive approach to valuing projects with managerial flexibility or real options. The discrete-time approach to real-option valuation has typically been implemented in the finance literature using a binomial lattice framework. Instead, we use a binomial decision tree with risk-neutral probabilities to approximate the uncertainty associated with the changes in the value of a project over time. Both methods are based on the same principles, but we use dynamic programming to solve the binomial decision tree, thereby providing a computationally intensive but simpler and more intuitive solution. This approach also provides greater flexibility in the modeling of problems, including the ability to include multiple underlying uncertainties and concurrent options with complex payoff characteristics.

Key words: decision analysis; real options; decision trees; binary approximations

1. Introduction

Discounted cash flow (DCF) methods are commonly used for the valuation of projects and for decision making regarding investments in real assets. One of the most important limitations of DCF is that it fails to account for the value of managerial flexibility inherent in many types of projects. The options derived from managerial flexibility are commonly called real options to reflect their association with real assets rather than with financial assets. Although appealing from a theoretical perspective, the practical use of real-option valuation techniques in industry has been limited by the mathematical complexity of these techniques and the resulting lack of intuition associated with the solution process, or the restrictive assumptions required to obtain analytical solutions.

In this article we outline how traditional decision analysis tools can be used as an alternative to solve real-option valuation problems based on the ideas suggested by Copeland and Antikarov (2001) and further illustrated in Copeland and Tufano (2004). We do this by using a binomial decision tree to determine the cash flows and probabilities that give the correct project values when discounted to each period and to each uncertain state. Project flexibilities, or real options, can then be modeled easily as decisions that affect these cash flows. This specification of project uncertainties, cash flows, and decisions allows the problem to be modeled and solved using commercially available decision tree software familiar to the decision analysis community. Our discussion expands on the ideas presented originally by Brandao and Dyer (2005) and illustrates the approach with several examples.

While many of these ideas are relatively straight-forward and build on concepts suggested by Nau and McCardle (1991) and Smith and Nau (1995), we hope to make this material more accessible to decision analysts and to encourage additional work on the relationship between decision analysis and finance. Triantis and Borison (2001) provide an assessment of the use of options-based project valuation methods in practice and conclude that a modest evolution is occurring within some companies to support their adoption. In particular, Triantis and Borison anticipate increasing convergence among the various realoption approaches, particularly the decision-analytic and option-pricing approaches. In that spirit we also review some basic option-pricing concepts that will be familiar to many readers but that are nonetheless included as a useful reference in the context of this discussion. We will also take care to discuss the underlying assumptions and limitations of these methods and to suggest when they might be a valuable addition to the decision-analysis tool kit when used appropriately.

The remainder of the article is organized as follows. Section 2 reviews the traditional approaches to project valuation. Section 3 outlines a decision tree approach to the real-option problem discussed by Copeland and Tufano (2004). Section 4 provides an extension of this approach to problems in which project cash flows over time are explicitly modeled and used as the basis for valuing real options. This approach is illustrated in [section]5 with a numerical example. In [section]6 we conclude with a discussion of the limitations of this approach and identify some areas for further research.

2. Background on Project Valuation

With the DCF approach to valuation, the net present value of a project is calculated by discounting the future expected cash flows at a discount rate that takes into account the risk of the project. In practice, this discount rate is often the weighted average cost of capital (WACC) for the firm, based on the assumption that both the firm and the project share identical market risks. While this assumption may be valid for projects that mimic the risks associated with the firm as a whole, it may not be appropriate for unusual or innovative investment projects. In such cases, the practitioner must exercise judgment in choosing an appropriate discount rate for the project. For a discussion of the issues associated with the selection of a project discount rate and the calculation of the WACC, see Grinblatt and Titman (1998, Chapters 10 and 12).

A major criticism of DCF is the implicit assumption that the project’s outcome will be unaffected by future decisions of the firm, thereby ignoring any value that comes from managerial flexibility. Management flexibility is the ability to make decisions during the execution of a project so that expected returns are maximized or expected losses are minimized. Examples of project flexibilities include expanding operations in response to positive market conditions, abandoning a project that is underperforming, deferring investment for a period of time, suspending operations temporarily, switching inputs or outputs, reducing the project scale, or resuming operations after a temporary shutdown. The incremental value of these options can only be determined using an option-pricing or decision analysis approach.

Option-pricing methods were first developed to value financial options. However, the potential application of these methods to the valuation of options on real assets was quickly identified, and hundreds of scholarly papers have been written on this topic. Nevertheless, applications of real-option valuation methods to practical problems have been limited by the mathematical complexity of the approach, by the restrictive theoretical assumptions required, and by their lack of intuitive appeal.

The mathematical complexity associated with real-option theory stems from the fact that the general problem requires a probabilistic solution to a firm’s optimal investment decision policy, not only at present but also at all instances in time up to the maturity of its options. To solve this problem of dynamic optimization, the evolution of uncertainty in the value of the real asset over time is first modeled as a stochastic process. Then the value of the firm’s optimal policy is a partial differential equation that is obtained as the solution to a value function represented by Bellman’s principle of optimality, where appropriate boundary conditions reflect the initial conditions and terminal payoff characteristics. When closed-form mathematical solutions are unavailable, which is usually the case for more complex problems where the project may be subject to several sources of uncertainty and more than one type of option, numerical methods and discrete dynamic programming must be used to obtain a solution.

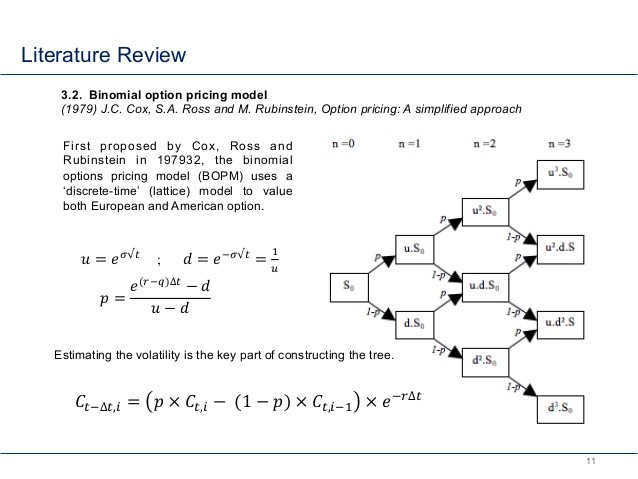
A discrete approximation to the underlying stochastic process can be developed to provide a transparent and computationally efficient model of the valuation problem. The first example of this approach is a binomial lattice model that converges weakly to a lognormal diffusion of stock prices, developed by Cox et al. (1979). A binomial lattice may be viewed as a probability tree with binary chance branches, with the unique feature that the outcome resulting from moving up (u) and then down (d) in value is the same as the outcome from moving down and then up. Thus, this probability tree is recombining, since there are numerous paths to the same outcomes, which significantly reduces the number of nodes in the lattice. A binomial lattice and the corresponding binomial tree are shown in Figure 1, where S is the current market price of the asset and q is the probability of an upward move to Su.

[FIGURE 1 OMITTED]

The binomial lattice model can be used to accurately approximate solutions from the Black-ScholesMerton continuous-time valuation model for financial options, with the added advantage of allowing a solution for the value of early-exercise American options, whereas the Black-Scholes-Merton model can value only European options.

Unfortunately, the process of working through lattices can be cumbersome and nonintuitive, especially for more complex applications to real assets, which can involve several simultaneous and compound options. The typical approach to using a lattice involves finding a replicating portfolio at each node. This approach is based on traditional option-pricing methods, which require that markets be complete in the sense that there are enough traded assets to allow the creation of a portfolio of securities whose payoffs replicate the payoffs of the asset in all states of nature and in all future periods. The assumption of the existence of a replicating portfolio underlies much of the initial work done in the field of continuous-time, real-option valuation by Brennan and Schwartz (1985), McDonald and Siegel (1986), Dixit and Pindyck (1994), and Trigeorgis (1996).

The use of traditional option-pricing methods and the replicating portfolio approach is complicated by the fact that, for most projects involving real assets, no such replicating portfolio of securities exists, so markets are incomplete. In this case, Dixit and Pindyck (1994) propose the use of dynamic programming using a subjectively defined discount rate, but the result does not provide a market value for the project and its options.

The application of decision analysis to real-option valuation problems seems natural because decision trees are commonly used to model project flexibility, but there has been limited work in this area (Howard 1996). Nau and McCardle (1991) and Smith and Nau (1995) study the relationship between option pricing theory and decision analysis and demonstrate that the two approaches yield the same results when applied correctly. Smith and Nau propose a method that integrates the two approaches by distinguishing between market risks, which can be hedged by trading securities and valued using option pricing theory, and private uncertainties, which are project-specific risks and can be valued using decision analysis techniques.

Smith and McCardle (1998, 1999) illustrate how this approach can be applied in the context of oil and gas projects and provide a discussion of lessons learned from applications to some case studies.

The distinction between market risks and project-specific risks is often a very natural one in oil and gas exploration projects, since oil and gas prices are market risks, while the project-specific risks may be the probability of a dry hole or the probability distribution regarding the volume of reserves.