In finance. return is a profit on an investment. [ 1 ] It comprises any change in value, and interest or dividends or other such cash flows which the investor receives from the investment.

Ambiguously, return is also used to refer to a profit on an investment, expressed as a proportion of the amount invested. This is also called the holding period return .

A loss instead of a profit is described as a negative return .

Rate of return is a profit on an investment over a period of time, expressed as a proportion of the original investment. [ 2 ] The time period is typically a year, in which case the rate of return is referred to as annual return .

Return, in the second sense, and rate of return, are commonly presented as a percentage.

ROI is an abbreviation of return on investment. i.e. return per dollar invested. It is a measure of investment performance, as opposed to size (c.f. return on equity. return on assets. return on capital employed ).

Contents

§ Calculation [ edit ]

The return, or rate of return, can be calculated over a single period, or where there is more than one time period, the return and rate of return over the overall period can be calculated, based upon the return within each sub-period.

§ Single-period [ edit ]

The return over a single period is:

where:

= final value, including dividends and interest = initial value

For example, if you hold 100 shares, with a starting price of 10, then the starting value is 100 x 10 = 1,000. If you then collect 0.50 per share in cash dividends, and the ending share price is 9.80, then at the end you have 100 x 0.50 = 50 in cash, plus 100 x 9.80 = 980 in shares, totalling a final value of 1,030. The change in value is 1,030 — 1,000 = 30, so the return is 30 / 1,000 = 3%.

Without any reinvestment, a return over a period of length is equivalent to a rate of return:

For example, 20,000 USD returned on an initial investment of 100,000 USD is a return of 20%. If the 20,000 USD is paid in 5 annual installments of 4,000 USD per year, with no reinvestment, the rate of return is 4,000 / 100,000 = 20% / 5 = 4% per year.

Assuming returns are reinvested however, due to the effect of compounding. the relationship between a rate of return , and a return over a period of length is:

which can be used to convert the return to a rate of return :

For example, a 33.1% return over 3 months is equivalent to a rate of:

per month with reinvestment.

Annualisation is the process of converting a return to an annual rate of return , where the length of the period is measured in years and the rate of return is per year.

§ Logarithmic or continuously compounded return [ edit ]

and the logarithmic rate of return is:

or equivalently it is the solution to the equation:

where:

= logarithmic rate of return = length of time period

For example, if a stock is priced at 3.570 USD per share at the close on one day, and at 3.575 USD per share at the close the next day, then the logarithmic return is: ln(3.575/3.570) = 0.0014, or 0.14%.

§ Annualisation of logarithmic return [ edit ]

Under an assumption of reinvestment, the relationship between a logarithmic return and a logarithmic rate of return over a period of time of length is:

so trivially is the annualised logarithmic rate of return for a return , where is measured in years.

For example, if the logarithmic return of a security per trading day is 0.14%, assuming 250 trading days in a year, then the annualised logarithmic rate of return is 0.14%/(1/250) = 0.14% x 250 = 35%

§ Returns over multiple periods [ edit ]

When returns are calculated over more than one time period, they are based on the investment value at the beginning of each period.

If the returns over successive time sub-periods are , then the cumulative return or overall return over the overall time period is:

If the returns are logarithmic returns however, the logarithmic return over the overall time period is:

§ Arithmetic average rate of return [ edit ]

The arithmetic average rate of return over time periods of equal length is defined as:

If you have a sequence of logarithmic rates of return over equal successive periods, the appropriate method of finding their average is the arithmetic average rate of return.

§ Geometric average rate of return [ edit ]

For ordinary returns, if there is no reinvestment, and losses are made good by topping up the capital invested, so that the value is brought back to its starting-point at the beginning of each new sub-period, use the arithmetic average return.

With reinvestment of all gains and losses however, the appropriate average rate of return is the geometric average rate of return over n periods, which is:

Note that the geometric average return is equivalent to the cumulative return over the whole n periods, converted into a rate of return per period.

In the case where the periods are each a year long, and there is no reinvestment of returns, the annualized cumulative return is the arithmetic average return. Where the individual sub-periods are each a year, and there is reinvestment of returns, the annualized cumulative return is the geometric average rate of return.

For example, assuming reinvestment, the cumulative return for annual returns: 50%, -20%, 30% and -40% is:

and the geometric average is:

which is equal to the annualized cumulative return:

§ Comparisons between various rates of return [ edit ]

§ External flows [ edit ]

In the presence of external flows, such as cash or securities moving into or out of the portfolio, the return should be calculated by compensating for these movements. This is achieved using methods such as the time-weighted return . Time-weighted returns compensate for the impact of cash flows. This is useful to assess the performance of a money manager on behalf of his/her clients, where typically the clients control these cash flows. [ 3 ]

§ Fees [ edit ]

To measure returns net of fees, allow the value of the portfolio to be reduced by the amount of the fees. To calculate returns gross of fees, compensate for them by treating them as an external flow, and exclude accrued fees from valuations.

§ Money-weighted rate of return [ edit ]

Like the time-weighted return, the money-weighted rate of return (MWRR) or dollar-weighted rate of return also take cash flows into consideration. They are useful evaluating and comparing cases where the money manager controls cash flows, for example private equity. (Contrast with the true time-weighted rate of return, which is most applicable to measure the performance of a money manager who does not have control over external flows.)

§ Internal rate of return [ edit ]

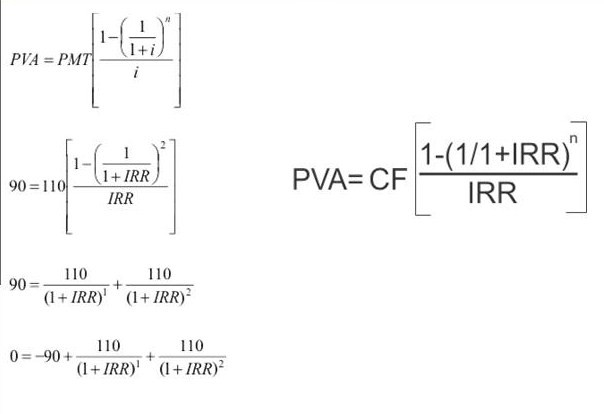
The internal rate of return (IRR) (which is a variety of money-weighted rate of return) is the rate of return which makes the net present value of cash flows zero. It is a solution satisfying the following equation:

where:

NPV = net present value

and

= net cash flow at time , including the initial value and final value , net of any other flows at the beginning and at the end respectively. (The initial value is treated as an inflow, and the final value as an outflow.)

When the internal rate of return is greater than the cost of capital. (which is also referred to as the required rate of return ), the investment adds value, i.e. the net present value of cash flows, discounted at the cost of capital, is greater than zero. Otherwise, the investment does not add value.

Note that there is not always an internal rate of return for a particular set of cash flows (i.e. the existence of a real solution to the equation depends on the pattern of cash flows). There may also be more than one real solution to the equation, requiring some interpretation to determine the most appropriate one.

§ Comparing ordinary return with logarithmic return [ edit ]

The value of an investment is doubled if the return = +100%, that is, if = ln($200 / $100) = ln(2) = 69.3%. The value falls to zero when = -100%. The ordinary return can be calculated for any non-zero initial investment value, and any final value, positive or negative, but the logarithmic return can only be calculated when .

Ordinary returns and logarithmic returns are only equal when they are zero, but they are approximately equal when they are small. The difference between them is large only when percent changes are high. For example, an arithmetic return of +50% is equivalent to a logarithmic return of 40.55%, while an arithmetic return of -50% is equivalent to a logarithmic return of -69.31%.

Comparison of ordinary returns and logarithmic returns for an initial investment of $100

Initial investment,