Put Call Parity And Prices Of European Put Finance Essay
Post on: 11 Июль, 2015 No Comment
People who have done financial mathematics before or worked in financial area must be familiar with a terminology called put-call parity. The put-call parity (PCP) describes the relationship between the prices of European put and call options with the same exercise price and time to maturity. It shows that the value of a European call with certain strike price and exercise date can be deduced from the value of a European put with the same strike price and exercise date, and vice versa. It is an option pricing concept that requires the value of call and put options to be in equilibrium to prevent arbitrage.
The concept of PCP is especially important when trading synthetic positions. When there is a mispricing between an instrument and its synthetic position, an options arbitrage opportunity exists. Arbitrageurs would step in to make profitable, risk-free trades until the departure from put-call parity is eliminated. Knowing how these trades work can give the investor a better feel for how put options, call options and the underlying stock are all interrelated.
1.2 Aims and objectives of the research
There are quite a lot studies on the test of the PCP. Tests of the put/call parity theory have yielded mixed results, though most have been supportive of the underlying concept. But in most of these tests, there had been a priori assumption that PCP theory was indeed valid. However, in reality, the extrinsic value of put and call options are rarely in exact parity in option trading even though market makers have been charged with the responsibility of maintaining PCP. When the outlook of a stock is bullish, the extrinsic value of call options tend to be higher than put options due to higher implied volatility and when the outlook of a stock is bearish, the extrinsic value of put options tends to be higher than call options.
This dissertation examines the basic validity of the PCP theory with no assumptions concerning its inherent validity and finds that PCP does not exist in the pricing of options contracts. Also, this dissertation is to work out the deviation from the put-call parity, investigates and explains the deviation by using econometric models. At last, the author will answer the question:”why does the put-call parity not hold?”
As mentioned in chapter 2, we know the PCP is an important financial definition. However, since the PCP was developed, large amount of tests had been carried out. Tests of the PCP theory have yielded mixed results, but majority of the tests had a similar result: the put-call parity was invalid.
3.1 The put-call parity was valid
As mentioned before, the PCP was developed by Stoll (1969) to establish a relationship between the prices of put and call options. However, later he recognised that in the real financial world, some factors like transactions costs and taxes could affect the results. By assuming the appropriate interest rate was the three-month Treasury rate and adding this rate into his data, Stoll tested two sets of data which were “regular companies” and “new business”. The results showed that there were problems with the coefficient of the interest rate term. He again recognised that there were some other factors could affect the interest rate term, so despite those the problems, Stoll then concluded that the PCP theory was reasonably valid.
By looking through previous studies, Klemkosky and Resnick (1979) found that these studies consisted with the PCP, they also pointed out that in the relationship some inefficiency found to exist (put call parity and market efficiency). However, the options market in 1979 is different from 10 years ago. They recognised that the structure of the options markets has been changed, therefore some of the previously noted defects needed to be amended. They added a dividend term into the original model. The empirical results showed that about half long hedges tests and short hedges tests were profitable. That means the models tested were consistent with the PCP theory. Later in 1980, Klemkosky and Resnick found that there was “perfect foresight” characteristic in their previous work, so they corrected their model by adding the time lag in. A number of hedges showed profitability as well. That was again concluded that PCP and market efficiency obtained.
There were still other studies which concluded the PCP was valid, however, according to the objects of this dissertation which was trying to find out the invalidation of the PCP theory, we are now focus on the studies which concluded the PCP was invalid.
3.2 The put call parity was invalid
3.2A The put call parity on the European options
Loudon (1988) tested the PCP by providing Australian evidence. He collected the data of the prices of identical put and call options together with the underlying share price from the Sydney Stock Exchange Market during the calendar year of 1985. The empirical results showed that observed violations of the theory are existed, which are the boundary violations. He did some analysis of these violations. He tested the effects of some factors: institutional factors, price non-simultaneity, transaction costs, stock price range, time to maturity and in or out of the money category. He found that these observed violations cannot be explained by the presence of non-simultaneous price data. There is no significant relationship was found between the extent of price non-simultaneity and observed violations. However, the existence of transaction costs shows to have the most significant influence on the violations observed.
Taylor (1990) found the violation from PCP by providing evidence of the pricing of options traded on the Australian Options Market (AOM). He collected AOM data for BHP and Woodside from 1982 to 1985. The derivation of put call relationship assumes frictionless markets, which mean transaction costs, differential of borrowing and lending rates and taxes are all assumed not to exist. He tested the PCP theory and found several evidences of violation of the parity conditions. But violations of this type were not that easy to develop after putting possible transaction costs into consideration. Although the existence of these violations cannot be explained by transaction costs, they do provide a rationale for their non-exploitation.
According to Guo and Su (2006), the original PCP may not apply to the heavily traded options on dividend-paying securities, because the original put-call parity relations assumed that the underlying security does not pay dividends before the expiration of the options. However, in the real economic world a mass of stocks and almost all stock indices pay dividends. Therefore, their tests were based on the reality that the underlying security pays dividends; they improved the put-call parity formula. The tests presented a variation of the relations when the underlying securities pay dividends. The results provided theoretical scopes for the options prices when the underlying stock pays dividend. Also the results spread out application of put-call parity relations to all options on currencies and dividend-paying stocks and stock indices.
Brunetti and Torricelli (2003) tested the PCP by focusing on a European market, the Italian Mib30 index option market (MibO), rather than on North American markets. They collected the data from the period 1 September 2002 to 31 December 2002. They tested the PCP in the total absence of frictions in the first step, and then in the second step they added the bid-ask spread into the analysis. Finally the commission costs had been included as well. The result showed that during the analysis period, the Mibo market was efficient. Also the role of frictions in the tests of the PCP has been stood out.
Ahn, Byoun and Park (2003) researched arbitrage opportunities of the KOSPI 200 options in Korea, a relatively new market but the fastest growing and the most actively traded index option market in the world. Their tests focus on the PCP conditions, such as: transaction costs. The data they used was composed of KOSPI 200 options from January 1998 to September 1999, but excluding the first several months because of possible unusual activities at the beginning section. They found that overall there were a reasonable quantity of violations of the PCP conditions. The frequency of violation ranges from 25.4% to 49.9% for different time periods.
Li (2006) focused on the arbitrage efficiency of the Nikkei 225 index options market in the Osaka Securities Exchange (OSE) with the purpose of providing evidence on the size and frequency of the arbitrage opportunities in the PCP framework. He investigated the arbitrage efficiency of the Nikkei 225 options market by using both an ex post and ex ante test. The ex post test showed that there 2.74 percent of the sample violations of the PCP and 22.62 index points arbitrage profit for the OSE firms. The ex ante test showed that both the two numbers are decreased because of time lag. Then Li used the regression analysis to support the ex post and ex ante tests results. To conclude, there was no strong evidence against the efficiency of the Nikkei 225 options market.
Kamara and Miller (1995) tested the PCP condition using European options to avoid the early exercise problem. They collected the data from the Standard and Poor’s 500 stock index traded on the Chicago Board Options Exchange (CBOE). By using daily and intra-daily prices, they found violations of PCP are much less frequent and smaller than those previously studies which using American options. The result showed that the deviations from PCP conditions are related to the liquidity risk in the stock and options markets. Therefore, the frequency and size of deviations increased with the increasing of liquidity risk. They pointed out that the bid prices of call and put options rise related to their PCP-implied bid prices and the ask prices fall related to their PCP-implied ask price. Moreover, the results suggest that the trading strategies underlying PCP are subject to significant liquidity risk.
3.2B Put-Call parity on the American options
There are few studies of PCP on the American options. Merton (1973) showed PCP need not hold for the American options because the possibility of early put exercise cannot be completely eliminated when the portfolio is established.
Evnine and Rudd (1985) used the S&P100 options and Major Markets Index (MMI) to test both European PCP and American PCP. The result showed that there were a significant number of potential profit opportunities. The call overpricing violations for both the S&P100 and MMI occurred throughout the period. The options frequently violate the arbitrage boundary and the PCP; also, the options are substantially mispriced relative to theoretical values.
Gould and Galai (1974) tested the PCP on securities by adding the transaction costs in. They found that the transactions costs must be assumed to make the model comply with the data. The basic model was supported after including rather large transactions costs. They also found that similar deviations from the efficient market hypothesis have shown up in related study by other researchers; however their explanations of these results appeared to be incorrect on theoretical scopes.
3.3 Deviations from the put-call parity
Any deviations from the PCP can be used by investors to make riskless profits.
Martijn and David (2007) investigated violation from PCP by using different implied volatility or volatility spread between call and put options with the same underlying price, the same strike price and the same expiration date. They found that deviations from PCP contain information about later coming stock prices. There was significant evidence of predictability. By controlling for size, they found that deviations from PCP are more possible to appear when underlying stocks face more information risk. Overall, they suggested that the price of an option could be affected by its demands.
Ariful, Meher and Geoffrey (2004) tested the impact of transactions cost on deviations from PCP properties. They used the foreign exchange options which traded on the Philadelphia Exchange (PHLX) from 01 August 2005 to 31 July 2006. By using the intra-daily option, they studied the impact of alternative measures of transaction cost on PCP deviations. Three measures of transaction costs were used: first, a minimum transactions cost that involve only initial bid-ask spreads; second, transaction costs associated with trades closed out prior to expiration; and third, a total transaction costs measure. The results indicated how transactions costs can impact the interpretation of deviations from PCP.
3.4 Summary
As mentioned previously, there were many studies on the PCP; most of them had a similar result which indicated that the PCP was not hold in the real financial society. The transaction costs are one of the reasons that had been showed in most of the studies.
Also, there are deviations from the PCP. Any deviations from the PCP can be used by investors to make riskless profits. Some studies indicated that transaction costs can impact the interpretation of deviations from the PCP.
Chapter 4 Methodology
This chapter describes the methodology in the study and the procedures for data collection and data analysis. Methodology includes the following concepts as they relate to a particular discipline or field of inquiry: a collection of theories, concepts or ideas; comparative study of different approaches; and critique of the individual methods. Methodology refers to more than a simple set of methods; rather it refers to the rationale and the philosophical assumptions that underlie a particular study relative to the scientific method.
In this dissertation, the author is going to test the put-call parity by using the most recently options data. The author will work out the deviation from the put-call parity. By using the deviation as a dependent variable and put into a simple regression model, the author will find the factors that can affect the deviation. Also, the author will explain the bid and offer price which appear in the data.
4.1 The regression model
Regression models are used to predict one variable from one or more other variables. Also, regression models provide the scientist with a powerful tool, allowing predictions about past, present, or future events to be made with information about past or present events.
In order to explain the deviation from put-call parity, the author uses a regression model. The model is as the following:
In this regression model, diff (the deviation) is the dependent variable, τ (time to expiry), r (risk-free rate), St (the current price of the underlying), and K (strike price) are the explanatory variables. The error term is û.
The deviation (diff) is the difference between the two portfolios in the put-call parity. As what has been mentioned in chapter 2, Portfolio A is the call option + an amount of cash equal to K*exp (-r*τ); Portfolio B is the put option + one share. Let diff = Portfolio B – Portfolio A = (p + St)-(c + K*exp (-r*τ)). If diff is positive, that means portfolio B is over-priced relative to portfolio A, and vice versa.
It is obvious that the put-call parity does not hold in the real economic world, there might be some reasons. By doing a simple regress on the above model, the author will find out which explanatory has significant effect on the dependent variable.
In the option data the author collected, there are two different option prices, the bid and offer. So the above model will change to the following two models:
4.2 The option data
The author is going to briefly describe the option data that has been used in the test of put-call parity.
The European option data that used in the test is called CBOE RUSSELL 2000 INDEX-RUT. The CBOE Russell 2000 (RUT) Index is a leading benchmark for the performance of small-capitalization stocks. The CBOE Russell 2000 Index was created in 1984 by Frank Russell Company and was designed to track the performance of small-cap companies. RUT options make it simple to participate in the small-cap market. (COBE website, 2010) All the European options started at 1 to 30 April 2009, with variety τ (time to expiry) from 2days to 626days.
The American option data that used in the test is called AFLAC INC. AFLAC Incorporated (AFLAC) is a general business holding company and acts as a management company, overseeing the operations of its subsidiaries. AFLAC sells supplemental health insurance policies to more than 40 million people worldwide. Because 80 percent of the company’s sales are made in Japan, it has been asking the federal government to pressure Japan to open its insurance markets to more competition. The company also lobbies on a variety of health care issues, including the battle over escalating prescription drug prices. (Open Secrets, 2010) All the American options started at 1 to 30 April 2009, with variety τ (time to expiry) from 1days to 661days.
The risk-free rate that is used in the model is the LIBOR rate. However, only up to one year LIBOR rate can be found, thus, the author left the options with more than 365days time to expiry out of the data. Then the τ of all the European options is from 2 to 353, and τ of all the American options is from 2 to 290.
4.3 Summary
In this dissertation, the models are the main tool to investigate the topic. The stata is the main software that used in this dissertation. The most important models are only four, they are:
Also, the author described the data that used in the dissertation, which are the most recently data collected from the yahoo finance. The LIBOR rate is also an important variable in doing the tests. The author collected the LIBOR rates from the ECOWIN, and used them into the tests.

5.3 Bid and Offer price
The bid is the highest price that a prospective buyer is willing to pay for a specific security. The offer, also called the asking price, is the lowest price acceptable to a prospective seller of the same security. The highest bid and lowest offer are quoted on most major exchanges, and the difference between the two prices is called the bid-ask spread. The bid-offer spread is the amount by which the ask price exceeds the bid. This is essentially the difference in price between the highest price that a buyer is willing to pay for an asset and the lowest price for which a seller is willing to sell it. The size of the bid-offer spread in a security is one measure of the liquidity of the market and of the size of the transaction cost.
In the test of the European options, some differences had been showed between these two prices which are unexpected. Look back Figure 5.4, when bid prices are taken into the test, it was found that the deviation from PCP rises monotonically with increase in τ. However, when offer prices had been used in the test, things changed. The deviation from PCP rises at a decreasing rate in τ, and there is a peak point that the differences would start decreasing from that point if the time to expiry (τ) keeps on increasing.
The previous studies had looked at similar difference in unexpected differences found in the test show here. Kalman and Steven (1981) found transaction costs causes bid-offer spreads. Also, Thomas and Francis (1993) examined the cross-sectional distribution of bid-ask spreads in the S&P 100 index options market, in which they found cross-sectional differences in bid-ask spreads are directly related to differences in market-making costs. According to Harold (1968), the bid-offer spread is a recognised measure of liquidity costs in exchange traded securities and commodities. Almost all of the transaction cost, such as: brokerage fees and bid-ask spreads are contained in the two elements of any orthonormal exchange. Under rival conditions the bid-ask spread measures the transaction costs immediately. The liquidity cost is the difference in price paid by an urgent buyer and received by an urgent seller. Because brokerage commissions do not vary with the time taken to complete a transaction, differences in bid-ask spread indicate differences in the liquidity cost.
Therefore, after the above discussing, it can be concluded that the unexpected difference between bid and offer prices appeared in the previous tests is because of the transaction costs. The transaction costs can be measured by the bid-offer spreads.
5.4 Summary
The author did the tests in order to find out the deviations from the PCP and discuss and explain these deviations.
In focusing on the relationship between time to expiry and differences, it is showed that the longer the time to expiry, the larger the deviations, ceteris paribus. Thus, the deviations from put-call parity are more likely to occur in options with underlying stocks that face more information risk because the longer the time to expiry, the more risk need faced.
At the end, the author explained the bid and offer prices, which caused the unexpected results during the tests.
Chapter 6 Conclusion
By looking at what has been previously discussed and all the results, the author can draw following conclusion:
The PCP does not hold for both European and American options used in the research. The differences (diff_bid and diff_offer) between the two portfolios, A and B, are positive or negative, never zero.
There is always deviation from the PCP. From the above research, when use the deviation from the PCP as a dependent variable in a model, there is evidence that all the explanatory variables in the model have significant effects on the dependent variable.
European option:
diff_bid = -18.5974** + 20.4371**τ — 0.9803**r + 0.0477**St – 0.0060**K
diff_offer = -22.1961** + 5.7477**τ + 2.0043**r + 0.0402**St + 0.0085**K
American option:
diff_bid = -0.4627** + 1.1301**τ + 0.0643**r + 0.0173**St + 0.0013**K
diff_offer = -0.5666** + 0.9446**τ + 0.1312**r + 0.0020**St + 0.0175**K
** indicates strong significance (p-value < 0.01)
This dissertation is interested in the effect of the time to expiry (τ) The results show there is evidence that time to expiry is positive significance, which the longer the time to expiry, the larger the deviations, ceteris paribus. There is an increasing heteroscedasticity relation between deviations and the time to expiry (τ), which would causes the incorrect of standard errors, t-rations and confidence intervals. Through using an option called “robust” to correct the standards errors regardless of the form of the heteroscedasticity.
Also, the results showed a non-linear relation between deviations and the time to expiry (τ) when the squared of time to expiry (τ²) was added into models. There is evidence that τ² is also significant, but the effects are different depends on the option prices. There is evidence that τ² has negative effect on the deviations from the chosen American option whatever the prices are. However, evidence showed that τ² has positive effects on the deviations from the chosen European option when the bid prices had been used and the effects are negative when the offer prices have been used.
Later, after using a single polynomial regression model to work out the peak point of the difference at a certain time to expiry (τ), the results showed that, for the European option, when taken bid price, the τ is a negative number which is impossible; when taken offer price, the peak point is equal to 10.7762 at τ=1.2539. For the American option, peak point is 1.2090 at τ = 1.3955 when its bid price; peak point is 1.1775 at τ = 1.4115 when its offer price. At last, the author used the previous literature to explain the unexpected differences showed in the results.
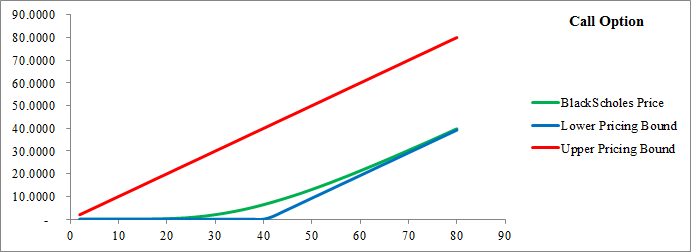
The failure of the PCP relationship has implications to asset pricing models like the Black/Scholes option pricing model. When PCP is a theoretical basis of the pricing model, then the pricing model may need to be revisited to determine whether or not it can be improved.














