Rho is the change in option value that results from movements in interest rates.

The value is represented as the change in theoretical price of the option for a 1 percentage point movement in the underlying interest rate. For example, say you’re pricing a call option with a theoretical value of 2.50 that is showing a Rho value of .25. If interest rates increase from 5% to 6%, then the price of the call option, theoretically at least will increase from 2.50 to 2.75.

As seen in the above graph, option rho for calls and puts have a mirrored profile; calls move from zero to a positive number as the stock price increases while puts move from a negative number towards zero under the same circumstances.

Rho, however, is more about interest rate movements than the underlying price and hence you will see greater impacts of its value depending on the premium of the option. See the next graphs.

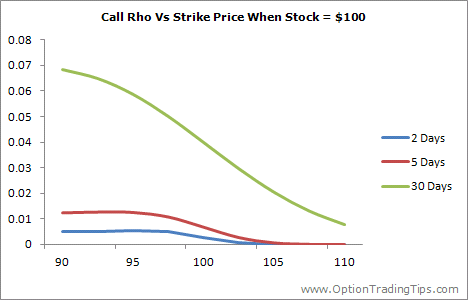
Stock Price = 100

Stock Price = 100

The above graphs, which plot the Rho of a call and a put option at 3 different points in time, across a range of strike prices, with a spot price of 100.

Unlike the other option greeks, Rho is larger for options that are in the money and decreases steadily as the option moves out of the money. Option Rho also increases with a greater amount of time to expiration.

These two factors are explained by the effect that interest rates have on the cost of carry of an option. ITM options, and options that have more time until expiration, will have higher premiums and therefore require more cash to hold the option until the expiration date.

Rho is generally the least important of all the option greeks. This is because option traders tend to focus on trading options that are close to expiration and out of the money.

The effect that interest rates have on option contracts is different for both call and put options.

There are two ways that interest rates affect option prices: the forward price and the premium discounting.

Forward Price

When calculating the price of an option, the first thing traders have to determine is what the price of he underlying asset will be at the expiration date. This is known as the forward price. Although an option trader can never know what this price will be, all other things being equal, it must be worth at least the cost of holding the asset until the expiration date. This value takes into account the cost of money i.e. what it would cost you in real terms to borrow and invest in the asset until the expiration date. This value, also refered to as the cost of carry, uses the current interest rate to determine how much additional capital you will need to hold the asset until the expiration date.

Take a look at this spreadsheet to see how the forward price is calculated:

Forward Price Calculator

For call and put options, the cost of carry has different effects on the price of the option. As interest rates increase, the forward price of the asset also increases, however, the effect on the option premium differs for calls and puts. For call options, the premium of the option increases as the forward price increase, but for put options the premiums decrease as the forward price increases. As interest rates decrease, call options will decrease in value and put options will increase with changes in the forward price.

Discounting Factor

The second way that interest rates effect the pricing of option contracts is in the discounting of the premium.

The price of an option contract is a future value. I.e. it estimates what the value of the instrument will be at some date in the future.

So, when you buy an option contract you are outlaying money today in order to receive some value in the future. When you do this you have to consider what this investment is going to cost you over the life of the option.

In other words,what is the value of the option in today’s terms?

To calculate this, we do what is called discounting or calculating the present value of the option. Here’s a spreadsheet to illustrate.

Discount Factor Calculator

It basically comes down to the finance principle a dollar today is worth more than a dollar tomorrow.