This article may be too technical for most readers to understand. Please help improve this article to make it understandable to non-experts. without removing the technical details. The talk page may contain suggestions. (November 2014)

In finance. the net present value (NPV ) or net present worth (NPW ) [ 1 ] is defined as the sum of the present values (PVs) of incoming and outgoing cash flows over a period of time. Incoming and outgoing cash flows can also be described as benefit and cost cash flows, respectively. [ 2 ]

Time value of money dictates that time has an impact on the value of cash flows. Cash flows of nominal equal value over a time series result in different effective value cash flows that makes future cash flows less valuable over time. If for example there exists a time series of identical cash flows, the cash flow in the present is the most valuable, with each future cash flow becoming less valuable than the previous cash flow. Thus, a cash flow today is more valuable than an identical cash flow in the future. [ 3 ] This decrease occurs because the discount factor represents the expected rate of return of each cash flow in a different investment with identical risk. With each additional period, the present value of a subsequent future cash flow decreases.

The NPV of an investment is determined by calculating the present value (PV) of the total benefits and costs which is achieved by discounting the future value of each cash flow (see Formula). NPV is a useful tool to determine whether a project or investment will result in a net profit or a loss because of its simplicity. A positive NPV results in profit, while a negative NPV results in a loss. The NPV measures the excess or shortfall of cash flows, in present value terms, above the cost of funds. [ 4 ] In a theoretical situation of unlimited capital budgeting a company should pursue every investment with a positive NPV. However, in practical terms a company’s capital constraints limit investments to projects with the highest NPV whose cost cash flows do not exceed the company’s capital. NPV is a central tool in discounted cash flow (DCF) analysis and is a standard method for using the time value of money to appraise long-term projects. It is widely used throughout economics. finance. and accounting .

In the case when all future cash flows are incoming (such as the principal and coupon payment of a bond ) the only outflow of cash is the purchase price, the NPV is simply the PV of future cash flows minus the purchase price (which is its own PV). NPV can be described as the “difference amount” between the sums of discounted cash inflows and cash outflows. It compares the present value of money today to the present value of money in the future, taking inflation and returns into account.

The NPV of a sequence of cash flows takes as input the cash flows and a discount rate or discount curve and outputs a price. The converse process in DCF analysis — taking a sequence of cash flows and a price as input and inferring as output a discount rate (the discount rate which would yield the given price as NPV) — is called the yield and is more widely used in bond trading.

Contents

§ Formula [ edit ]

Each cash inflow/outflow is discounted back to its present value (PV). Then they are summed. Therefore NPV is the sum of all terms,

where

– the time of the cash flow – the discount rate (the rate of return that could be earned on an investment in the financial markets with similar risk.); the opportunity cost of capital – the net cash flow i.e. cash inflow – cash outflow, at time t. For educational purposes, is commonly placed to the left of the sum to emphasize its role as (minus) the investment.

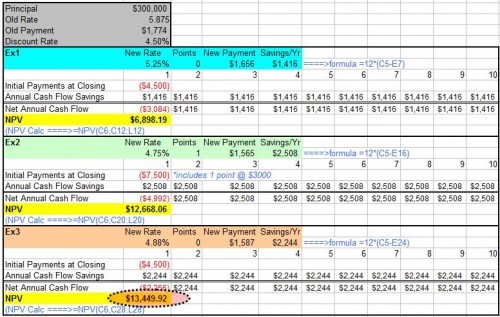
The result of this formula is multiplied with the Annual Net cash in-flows and reduced by Initial Cash outlay the present value but in cases where the cash flows are not equal in amount, then the previous formula will be used to determine the present value of each cash flow separately. Any cash flow within 12 months will not be discounted for NPV purpose, nevertheless the usual initial investments during the first year R ₀ are summed up a negative cash flow. [ 5 ]

Given the (period, cash flow) pairs (, ) where is the total number of periods, the net present value is given by:

§ The discount rate [ edit ]

The rate used to discount future cash flows to the present value is a key variable of this process.

A firm’s weighted average cost of capital (after tax) is often used, but many people believe that it is appropriate to use higher discount rates to adjust for risk, opportunity cost, or other factors. A variable discount rate with higher rates applied to cash flows occurring further along the time span might be used to reflect the yield curve premium for long-term debt.

Another approach to choosing the discount rate factor is to decide the rate which the capital needed for the project could return if invested in an alternative venture. If, for example, the capital required for Project A can earn 5% elsewhere, use this discount rate in the NPV calculation to allow a direct comparison to be made between Project A and the alternative. Related to this concept is to use the firm’s reinvestment rate. Reinvestment rate can be defined as the rate of return for the firm’s investments on average. When analyzing projects in a capital constrained environment, it may be appropriate to use the reinvestment rate rather than the firm’s weighted average cost of capital as the discount factor. It reflects opportunity cost of investment, rather than the possibly lower cost of capital.

An NPV calculated using variable discount rates (if they are known for the duration of the investment) may better reflect the situation than one calculated from a constant discount rate for the entire investment duration. Refer to the tutorial article written by Samuel Baker [ 6 ] for more detailed relationship between the NPV value and the discount rate.

For some professional investors, their investment funds are committed to target a specified rate of return. In such cases, that rate of return should be selected as the discount rate for the NPV calculation. In this way, a direct comparison can be made between the profitability of the project and the desired rate of return.

To some extent, the selection of the discount rate is dependent on the use to which it will be put. If the intent is simply to determine whether a project will add value to the company, using the firm’s weighted average cost of capital may be appropriate. If trying to decide between alternative investments in order to maximize the value of the firm, the corporate reinvestment rate would probably be a better choice.

Using variable rates over time, or discounting guaranteed cash flows differently from at risk cash flows, may be a superior methodology but is seldom used in practice. Using the discount rate to adjust for risk is often difficult to do in practice (especially internationally) and is difficult to do well. An alternative to using discount factor to adjust for risk is to explicitly correct the cash flows for the risk elements using rNPV or a similar method, then discount at the firm’s rate.

§ Use in decision making [ edit ]

NPV is an indicator of how much value an investment or project adds to the firm. With a particular project, if is a positive value, the project is in the status of positive cash inflow in the time of t. If is a negative value, the project is in the status of discounted cash outflow in the time of t. Appropriately risked projects with a positive NPV could be accepted. This does not necessarily mean that they should be undertaken since NPV at the cost of capital may not account for opportunity cost. i.e., comparison with other available investments. In financial theory, if there is a choice between two mutually exclusive alternatives, the one yielding the higher NPV should be selected.