Introducing QuantLib: Duration and Convexity

In this post Im going to explore QuantLibs support for assessing the riskiness of a bond. The riskiness of a bond is closely related to the magnitude of the bonds change in price given a small change in the bonds interest rate, which can be quantified to varying degrees of accuracy by calculating a bonds duration and convexity.  These interest rate sensitivity measures are fundamental to classical fixed income risk management. With knowledge of a bond or bond portfolios duration and convexity, a hedge can be executed to neutralize the effect of changes in the interest rate environment.  Moreover, the riskiness of bonds with different yields, coupon rates and maturities can be compared using a common set of benchmarks.

As weve seen already, a bonds price moves inversely to the bonds interest rate. When interest rates go up, a bonds price goes down and vice versa.  This relationship however, is not linear.  A bonds price increases at an increasing rate as bond prices fall and at a decreasing rate as bond prices rise as depicted in the figure below:

Duration and convexity seek to quantify the dynamics of the price versus yield relationship.

Lets dive deeper into the concept of duration . There are two flavors of duration: Macaulay duration and modified duration. The formula for calculating Macaulay duration, where C = coupon, r = interest rate, P = bond price, F = the bonds face value and n is the number of periods is:

Macaulay_Duration  = ( C1/(1+r) + 2*C2/(1+r)^2 +  n * (Cn+F)/(1+r)^n)/P

Macaulay duration can be understood as a bonds time-weighted average time to maturity.  A bond with a higher duration pays more of its cash flows further out in the future than a bond with a lower duration.  Another way of saying this is that the holder of a bond with a lower duration will get repaid more quickly than the holder of a bond with a higher duration.

Effectively, due to the time value of money, a bond with a higher Macaulay duration is more sensitive to interest rate changes than a bond with a lower Macaulay duration. This is attributable to the fact that cash flows discounted over a longer period of time have more effect on the bonds present value than near term cash flows.

Modified duration is closely related to duration and can be computed from it. Conceptually, it is equivalent to the slope of the line tangent to the curve in the figure above.  As such, it is a first-order sensitivity measure that is only accurate for small changes in the bonds interest rate.  Modified duration is derived from Macaulay duration in accordance with the following formula:

Dmod = Macaulay_Duration/(1+r)

Alternatively, since the modified duration is the slope of the line tangent to the bond pricing function, one can also compute modified duration by taking the derivative of the bond pricing formula and dividing by the bonds price:

Dmod = 1/P * dP/dr

Modified duration can be applied to calculate the change in a bonds price for a given change in the bonds interest rate like so:

Change_in_P =  Dmod * Change_in_r,  where Dmod is a negative quantity reflecting the inverse relationship of bond price and yield:

As previously mentioned,  duration is a linear, first-order measure of interest rate sensitivity.  Consequently, it overestimates the effect of an increase in rates on a bonds price and, conversely, underestimates the price impact of a drop in rates.  To more accurately quantify a bonds pricing relationship to its yield, the curvature of the bond pricing function must be accounted for.  This is accomplished with our second measure of interest rate sensitivity, convexity.  Convexity is a second-order measure of interest rate sensitivity.  As such, convexity is calculated by taking the second derivative of the bond pricing function and dividing by the bonds price:

Convexity = 1/P * dP2/dr2

To reprice a bond using both duration and convexity use the following formula, which is more accurate than using (modified) duration alone:

Change_in_P = P * ( Dmod * Change_in_r + .5 * Convexity * Change_in_r ^ 2)

To illustrate these duration and convexity formulas and provide independent verification of QuantLibs interest rate sensitivity calculations, I used Maxima, an open-source computer aided algebra (CAA) package. Maximas support for manipulating symbolic equations is similar to the commercial software products Mathematica and Maple.  At some point, I will do a series of posts on  Maxima, but for now, those of you who are curious about the meaning of the Maxima code to follow will have to rely on Maximas documentation:

Standard bond pricing formula:

bondprice(r,c,t,f):=(sum(c*f/(1+r)^i,i,1,t-1) + (c*f+f)/(1+r)^t);

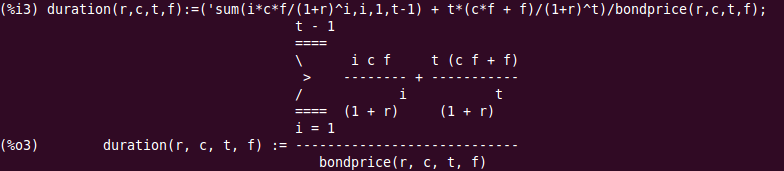
Macaulay duration time weighted average maturity of the bond:

duration(r,c,t,f):=(sum(i*c*f/(1+r)^i,i,1,t-1) + t*(c*f + f)/(1+r)^t)/bondprice(r,c,t,f);

Modified duration calculated by dividing Macaulay duration by (1 + r) and multiplying by -1:

dmod(r,c,t,f,p):=-1* duration(r,c,t,f)/(1+r);

Modified duration (alternative derivation) calculated by taking the derivative of the bonds pricing formula and dividing by the bonds price:

dbondprice:diff(bondprice(r,c,t,f),r);

dmod2(r,c,t,f):=ev(dbondprice,r=r,c=c,t=t,f=f)/b ondprice(r,c,t,f);

dconvexity:diff(bondprice(r,c,t,f),r,2);

QuantLib provides support for calculating duration, convexity, and several other measures of interest rate sensitivity, through its BondFunctions class. Lets see how to  how to calculate a bonds duration and convexity with QuantLib:

yield to maturity: 0.03

Macaulay duration: 2.8635

Modified duration: -2.7801

Convexity: 10.6258

Estimated bond price using only duration (rate up .01): 102.72

Estimated bond price using duration and convexity (rate up .01): 102.78

Lets compare the duration and convexity numbers to the what the Maxima equations produce:

That brings this post to a close. I hope you have gained a new appreciation for how duration and convexity are employed to help assess the riskiness of a bond and reprice a bond when interest rates change. Until next time, have fun with QuantLib!