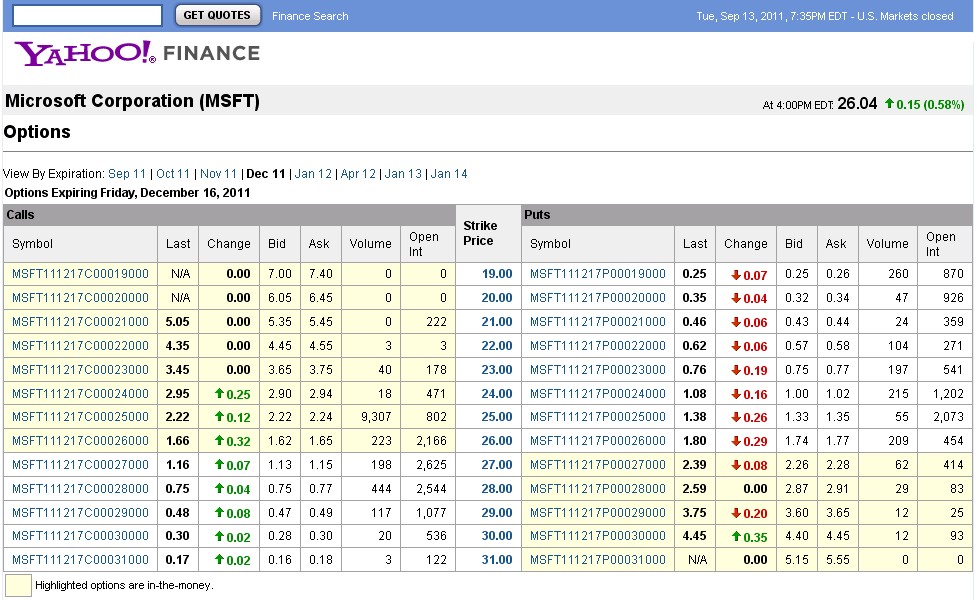
How do you use the putcall parity formula
Post on: 11 Июль, 2015 No Comment
Related Topics
The Put-Call parity is widely used to find discrepancies in the options market – mostly using computers to spot any arbitrage opportunities. In the earlier days, it was the bread and butter of option arbitrageurs. Of course, it is only valid for European options.
To understand how, first it’s important to understand how it works. Consider the following two portfolios:
Portfolio A: One European call option with strike K, plus an amount of cash equal to K e^ (-rT) (which is just K dollars at expiry time-discounted to today’s value).
At the expiration of the option, either:
(i) The call is in the money: So you exercise the call, you pay K dollars and receive the share.
(ii) The call is out of the money: You don’t exercise and are left with K dollars.
So either you own the share or K dollars, depending on whether the stock price is greater than K on expiry. Mathematically, your payoff is Max (S, K).
Portfolio B. One European Put option with strike K plus one share.
At the expiration of the option, either:
(i) The put is in the money: So you exercise the put. You receive K dollars and give them the share.
(ii) The put is out of the money: You don’t exercise and are left with the share.
So either you own K dollars or the share, depending on whether the stock price is lower than K on expiry. Mathematically, your payoff is Max (S, K).
As you can see, both the portfolios have the same value at expiry. Because the options are European, they can’t be exercised before expiry. So the portfolios must have identical values today.
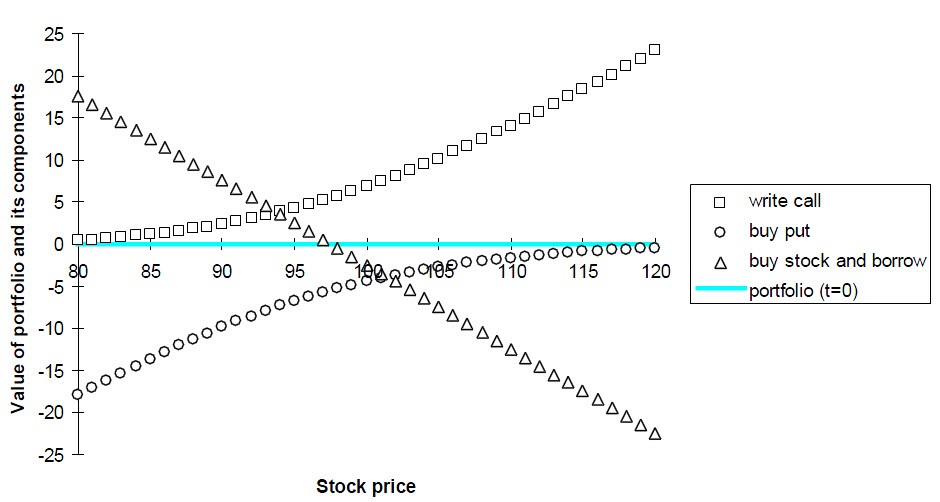
This means that the sum of a call and cash worth discounted strike price is equal to the sum of a put and a share (for the same strike).
Or, C + K e^ (-rT) = P + S
The key is that this relationship must always be valid.
So assuming you’re an arbitrageur, at any point in time, the variables K, r, T and S are always known. Now, in case the value of P is inflated over what it should theoretically be, you would sell the Right Hand side of the equation (which is more expensive) i.e. sell the put and the share and receive cash, and buy the Left Hand side of the equation (which is cheaper) i.e. buy the call. You'll be left with excess cash which will be your profit (after accounting for the strike you'd need to pay)
Your profit would be P + S – C – K e^ (-rT). (Right Hand minus Left Hand of the equation)
It’s straightforward to account for dividends and borrow rate too.
This arbitrage was ubiquitous when options were initially introduced. Of course, after the advent of technology and knowledge of option pricing, this arbitrage has mostly disappeared.














