WHAT IS GAMMA?

Gamma is the ugly step child of option greeks. You know, the one that gets left in the corner and no one pays any attention to it? The problem is, that step child is going to cause you some real headaches unless you give it the attention it deserves and take the time to understand it.

Gamma is the driving force behind changes in an options delta. It represents the rate of change of an option’s delta. An option with a gamma of +0.05 will see its delta increase by 0.05 for every 1 point move in the underlying. Likewise, an option with a gamma of -0.05 will see its delta decrease by 0.05 for every 1 point move in the underlying.

KEY POINTS REGARDING GAMMA

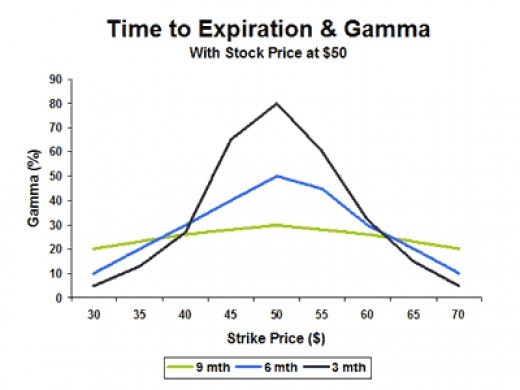
Gamma will be higher for shorter dated options. For this reason, the last week of an options life is referred to as “gamma week”. Most professional traders do not want to be short gamma during the last week of an options life.

Gamma is at its highest with at-the-money options.

Net sellers of options will be short gamma and net buyers of options will be long gamma. This makes sense because most sellers of options do not want the stock to move far, while buyers of options benefit from large movements.

A larger gamma (positive or negative) leads to a larger change in delta when your stock moves.

Low gamma positions display a flatter risk graph, reflecting less fluctuation in P&L.

High-gamma positions display a steeper risk graph, reflecting high fluctuation in P&L.

HOW GAMMA WORKS – RELATIONSHIP WITH DELTA

To get an idea of how gamma and delta work together, we will compare an at-the-money and an out-of-the-money call option. In the picture below you can see that a 10 lot at-the-money call position has a positive delta of 524 and a gamma of positive 62. The 185 call position has a delta of 86 and a gamma of 29. The gamma for the at-the-money position is significantly higher.

On the right side of the picture is a custom scenario. Assuming SPY has risen by 1% and all other factors remain the same (volatility, time to expiry, dividends). The delta for the 177 calls has risen by 107 to 631 whereas the 185 calls have only risen by 65. (Note that on a percentage basis the 185 calls had a bigger rise, but in terms of actual delta exposure, the 177’s had a bigger increase)

We can do the same analysis using long calls with different expiry months. Here you can see that the Dec 177 calls have a delta of 525 and a gamma of 63.  The June, 2014 177 calls have a similar delta at 501, but a much lower gamma at 21. Again, assuming a 1% change in price, you can see that the Dec calls have picked up an extra 107 delta and the June calls have only picked up an extra 38 delta.

The above analysis confirms that at-the-money options have higher gamma risk than out-of-the-money options and shorter dated options have higher gamma risk than longer dated options .

HOW GAMMA WORKS – RELATIONSHIP WITH VEGA

The gamma of an option will also be affected by Vega. When implied volatility on a stock is low, the gamma of at-the-money options will be high, while the gamma of deep out-of-the-money options will be near zero. This is because, when volatility is low, deep out-of-the-money options will have very little value as the time premium is so low. However, option prices rise dramatically on a relative basis, as you move back along the option chain towards the at-the-money strikes.

When volatility is high, and option prices are higher across the board, gamma tends to be more stable across the option strike prices. When volatility is high, the time value embedded in the deep out-of-the-money options can be quite high. Therefore as you move from the outer strikes back towards the at-the-money strikes, the increase in time value is less dramatic.

This concept is probably best explained visually. In the table below you can see the gamma of SPY calls when volatility is low (VIX at 12.50) and high (VIX at 25.00). The variation in gamma across the strikes is much smoother when volatility is high. Therefore, you can assume that the gamma risk of at-the-money options is much higher when volatility is low .

Here is the same data represented graphically. You can see when implied volatility is low, the gamma risk is much higher for the at-the-money strikes.

GAMMA AND OPTION STRATEGIES

So far we have only looked at individual options strikes. However, every option combination strategy will also have a gamma exposure. Trades that require you to be a net seller of options, such as iron condors, will have negative gamma, and strategies where you are a net buyer of options will have positive gamma. Below are some of the main options strategies and their gamma exposure:

GAMMA RISK EXPLAINED

In order to better illustrate how gamma works, I’ll look at a couple of different scenarios and compare how they are affected by a -2.0% move in price, with all other factors staying the same. I’ll look at their initial delta and their new delta after the move.

IRON CONDOR GAMMA RISK – COMPARING WEEKLY AND MONTHLY CONDORS

First up we have two iron condors with the short strikes set at delta 10. The weekly condor has a -4 gamma which is twice as high as the monthly condor at -2.

After a -2.0% move in the underlying, the weekly condors gamma has switched to positive and exploded out to 62, while the monthly delta has only moved to 20.

Clearly, the weekly condor has a much higher gamma risk. This is part of the reason why I do not like to trade weekly condors. A small move in the underlying can have a major impact on your position .

BUTTERFLY GAMMA RISK COMPARING WEEKLY AND MONTHLY BUTTERFLIES

Next we will look at butterfly spreads comparing weekly, monthly, narrow and wide butterflies.

Comparing a weekly and monthly 10 point butterfly, we have an interesting situation, with both trades basically having zero gamma at initiation. This is due to the fact that the short strikes were exactly at-the-money with RUT trading at 1101 at the time.

In any case, we see that with a -2.0% move in RUT, the weekly delta moves from -20 to +3 for a move of 23 points. The monthly delta moves from -4 to +3 for a total move of only 7 points.

Finally, let’s look at a 50 point wide at-the-money butterfly. The weekly butterfly has a whopping 146 point change in delta!  The monthly butterfly moves 73 points.

We can deduce from the above that weekly trades have a much higher gamma risk.  Butterflies have a higher gamma risk than iron condors and wide butterflies have the highest gamma risk of all the strategies. This is summarized below:

GAMMA SCALPING

Now that we know a bit more about gamma risk, let’s investigate a strategy you may have heard of called gamma scalping.

Gamma scalping is like that hot girl from high school that you were never good enough for.  The more you find out about her, the more amazing she sounds, but you don’t really know what makes her tick.

Gamma scalping is not for everyone for a number of reasons. For starters you have to be pretty well capitalized as it can be very capital intensive. Secondly, you need to have a very good understanding of how option greeks work before you even think about trading this way.

Many market makers make their livelihood by gamma scalping, so retail traders are naturally curious about this strategy, so that they can “trade like the pros”. The gamma scalping performed by market makers is an essential component of the efficient functioning of options markets as you will soon learn.

There are a few different ways you can set up a gamma scalp, but let’s look at an example using a long straddle.

IBM GAMMA SCALP USING LONG STRADDLE

Date: November 1, 2013

Current Price: $179.42

Trade Set Up:

Buy 2 IBM Jan 17 th 2014, 180 calls @ $4.35

Buy 2 IBM Jan 17 th 2014, 180 puts @ $5.65

Premium: $2,000 Net Debit

This trade set up gave us a net delta exposure of -13, so to get to delta neutral, we buy 13 shares.

Trade Set Up:

Buy 13 IBM shares @ $179.42

Cost: $2,332.46 Net Debit

Total Cost: $4,332.46

This trade will start out with a delta of zero, but it won’t stay that way. The reason is because of the positive gamma associated with the trade. In this case, the trade has a beginning gamma of +13. As the price of IBM fluctuates, the delta will change because of the gamma exposure. Being a positive gamma trade, price moves will benefit the trade. As IBM moves up, it will gain positive delta, as IBM moves down, the trade will pick up negative delta.

In order to get back to delta neutral each time, we would need to either buy or sell IBM shares. As the stock moves down, we gain negative delta and need to buy shares (buy low). As the stock moves up we sell shares (sell high) to neutralize delta. Notice that we are buying low and selling high. These transactions in the stock generate cash flow and can give rise to a profit providing the straddle does not lose too much value.