Compound Interest Formula

We use the compound interest formula when the interest we have collected at the end of a payment period is reinvested at the same rate as our original investment. Many bank accounts work in this way. Let’s look at an example.

Suppose you have $1,000 to invest at a bank that pays 12% compounded quarterly. At the end of the year. how much money would you have in your bank account?

Compounding quarterly simply means that you earn interest at the end of each quarter of the year. Since a year has 12 months, each quarter is made up of a 3-month period. So let’s say you started on January 1st and collect interest at the end of March (month 3/first quarter), June (month 6/second quarter), September (month 9/third quarter), and December (month 12/fourth quarter).

Using the simple interest formula. let’s calculate the amount in your account at the end of March, the first quarter:

The Simple Interest Formula

= Amount at the end of t years

= Principle

= Rate (as a decimal)

= Time in years

Derive by Example: Beginning with the Simple Interest Formula

So $1,030 is the new principal for the second quarter. Now, at the end of June, the second quarter, your account should have:

Similarly, at the end of the third quarter (September), the account will have:

And, finally, at the end of December, the fourth and last quarter, the account will have:

Notice that with compound interest you would earn an extra $5.51.

Analyzing Results

We’ll now take another look at those calculations and see if we can discover a pattern that will help us find the general formula for compound interest:

So it seems that at the end of n quarters, we’d have:

This is the same as

is what is known as the interest rate per quarter. Because interest rates are usually given as an annual nominal rate, we can find the rate per compounding period (per quarter in our example) by dividing the annual nominal rate r by the number of compounding periods per year m.

Finding the Pattern

So in general, if the principal P earns interest that is compounded m times a year at an annual rate of r. then:

End of the 1st period:

End of the 2nd period:

End of the 3rd period:

End of the nth period:

This leads us to the general formula.

The Compound Interest Formula

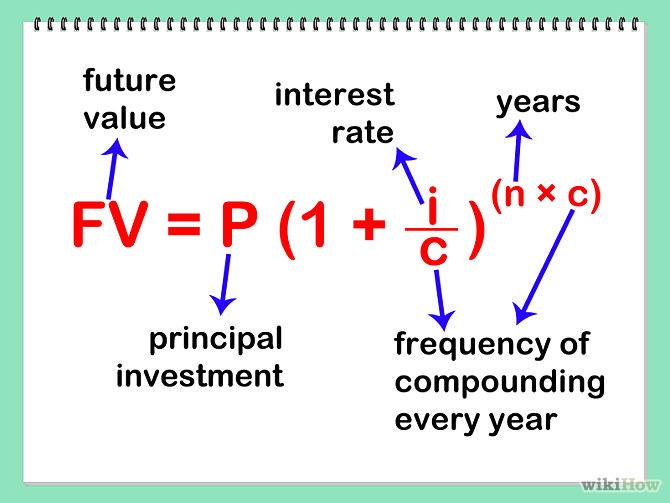
= Amount at the end of t years

= Principle

= Rate (as a decimal)

= # of compounding periods per year

= Time in years

= Total # of compounding periods

Examples

How much would you have in an account after 3 years if $2,000 was invested at an annual rate of 6% compounded monthly?

Find the values.

Plug values into the formula, and solve.

How much should you invest now at 10% to have $4,000 to purchase a car in 5 years if the interest is compounded quarterly?

Again, we will use the formula

Find the values.

Plug values into the formula, and solve.

So the initial investment of $2,441.08 will grow to $4,000 in 5 years.