Advertisement

Expert: Doug Ingram — 4/7/2000

Question

How would you describe the duration and the convexity of a T-bond? In what way(s) are these numbers useful? Also, how are these 2 numbers similar? Thank you very much for your time and help!

Answer

Unlike Weighted Average Life (WAL), which measures the amount of time that a bond’s principal is outstanding, duration also includes the interest coupons.

So one can roughly assume that the duration of a zero coupon or stripped (IO) bond is very close to the WAL and that the higher the coupon the lower (or shorter) the duration.

Duration is calculated by summing the present values of future cash flows times the period in which they occur and then dividing by the sum of the total cash flow.

Dur = (PvCf1 x 1 + pvCf2 x 2 + PVcf. n x n )/ PvCfTotal

In other words, we treat each future flow of Principal and Interest as an individual bond that matures x months out and then divide by that number.

That’s why a 2 year 0% has a duration and WAL near 0.

Portfolio managers use Modified Duration which is Duration dived by /(1+y) where y is the compounding yield. i.e. for a 6% bond, we would use 1.06 for annual, 1.03 for semi-annual, and 1.005 for monthly cash flows.

This number gives us a risk adjusted duration and helps us to identify exposure to interest rate shifts. Thus, a bond or portfolio with a 3 year (36 month) duration would lose about 3 points (3 %) of value if interest rates go up 100 bp (1% in basis points) or gain about 3% if interest rates fall by 100%. So the price change = -ModDur * interest change

In other words if we own a 6% bond with a modified duration near 2 years and interest rates go up by 2%, our bond value should drop by 4 points. Why? An investor can now get a 2 year duration bond near 8%. He would require 6% + 2% of discount for each year to achieve the same return.

100 + 8% + 8% + 0 discount = 116 vs. 100 + 6% + 6% + (4 points discount)

We also know then that a $50MM portfolio with a duration of 3 years should gain about $3MM in value if interest rates go down by 2%.

$50MM x (-3) x 2% = $3MM

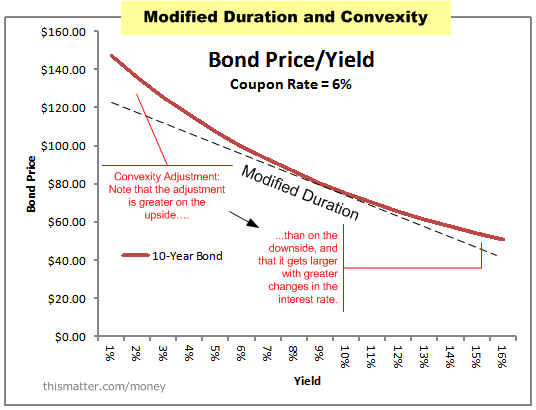
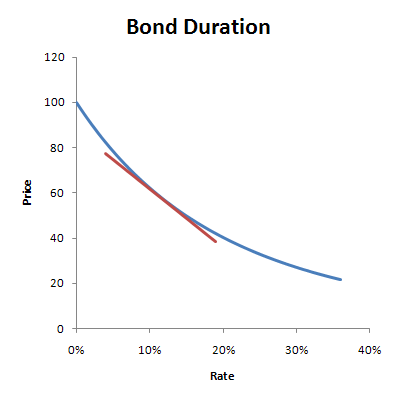
Bond prices rise faster as yields fall and they fall slower as yields rise. This convex shape is the derivative of duration that explains the part or the price sensitivity of a bond that is not explained by duration.

Picture a convex lens or bowl shape that shows prices rising faster or falling slower as yields go from very low to very high (left to right). Like the lens, convexity has more and more effect on a bonds price as yields move further away from the current yield. For small yield changes, duration explains almost all the risk. For larger yield shifts, we look to convexity.

They are similar in that they both explain price sensitivity to yield change. Bullet bonds (bonds with no options) always have this bowl or lens like shape which is termed positive convexity.

On more thing; if a bond is callable at a price like par, 101, or 102, it will resist appreciation in price above that call. Therefore, that bond displays negative convexity! This means the bowl shape is in effect as rates rise, but, as rates fall, the left side of the bowl turns over towards the call price. It’s no longer got that positively convex realtionship to yield change, and is therefore negatively convex.

Terms like effective duration are newer concepts that explain a little of the convexity issue in the duration formula. If a bond can lose 3 points if interest rates go up 100 bp, but only gains about .5 of a point if rates fall by 100 bp (because of a par (100) call), it has an effective duration of (3 + .5)/2 or 1.75. More on this if you wish, but that’s a simple answer.