The following article is reprinted from the Quarter 3, 2004

issue of On the Edge. the Interactive Data Fixed Income Analytics quarterly newsletter.

Effective Duration: Subtleties and Considerations

Teri Geske

Senior Vice President, Product Development

It is generally accepted that the effective duration of a bond is calculated by revaluing the security under higher and lower rate environments, where higher and lower are assumed to be parallel movements in interest rates of a certain magnitude, e.g. 25 bps, 50 bps or 100 bps. The average percentage change in the security’s value under the higher and lower rate environments relative to the starting value (adjusted for the magnitude of the shift) is the security’s effective duration. However, the specific implementation of this general definition can vary with respect to what is meant by interest rates, and the duration values that result will differ.

Beginning with version 5.21, BondEdge offers clients a choice of two methodologies in computing Effective Duration and Convexity, referred to as the Par Curve and Spot Curve methods. We have made this enhancement to offer total return managers a more consistent comparison with the values published by the purveyors of the major bond indices, who use the Par Curve method, while still retaining the Spot Curve method which we believe has a number of advantages as described later in the article. In previous newsletter articles we described the mechanics of these two methodologies, while in here we provide some comparisons and analyses to help portfolio managers understand these two approaches.

To summarize, the Par Curve method imposes parallel shifts on the initial Par bond yield curve and derives two new spot curves from the shifted par curves 1. These two resulting spot curves, each one derived from the shifted par bond yield curve, are used to value the security in the higher and lower rate environments, holding the security’s OAS constant. The average percentage change in the price of the security versus its current price is its Par Curve effective duration 2. In this case, while the yield curve shifts are parallel, the spot curves that are derived from the shifted yield curve are not parallel to the starting spot curve, except in the limiting case where the starting yield curve is flat.

The Spot Curve method, which has been the standard in BondEdge, first derives the initial spot curve from the current par curve, then imposes parallel shifts on the initial spot curve. Two new prices for the security are computed based on the shifted initial spot curve, holding constant the OAS derived from the starting price. The average percentage change in the price of the security computed this way is its Spot Curve duration. In this case, by definition, the shifted spot curves are parallel to the initial spot curve.

In both methods, the OAS for the security is derived from the initial spot curve, since OAS is the spread that must be layered onto a spot curve (not a yield curve) in order to equate the present value of the expected future cash flows to the market price of the security.

A few observations: (1) The shorter the maturity (or average life) of the security, the smaller the difference between the Par Curve and Spot Curve durations. Thus, for most MBS pass-throughs, ABS and short to intermediate corporate bonds this distinction is somewhat irrelevant. However, for long maturity bullet bonds and some CMOs, the difference can be substantial (a difference of 0.70 or more, in some cases). (2) A steep yield curve increases the difference between the two methods — a flat yield curve minimizes the difference. (3) In some cases, such as for zero-coupon bonds, the Par Curve method can produce non-intuitive results. (4) The Spot Curve method may be considered more internally consistent, because the bond’s OAS is derived from the same curve that is shifted to derive its Effective Duration.

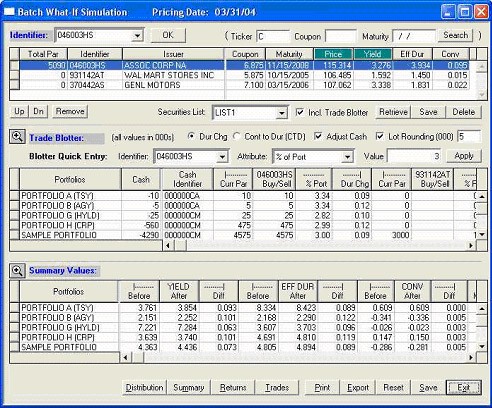
Consider the following examples (all based on market conditions as of month-end June 2004):