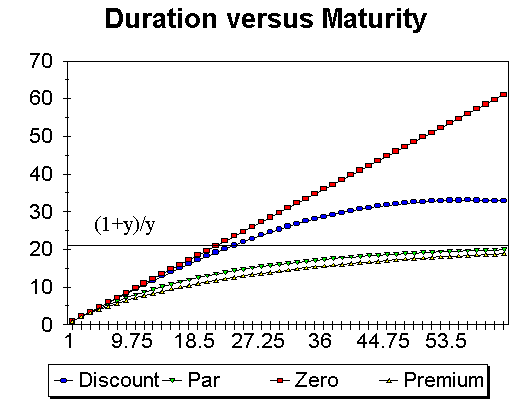
The interest rate risk covers the relation of changes in yield and bond price changes, primarily based on the concepts of duration and convexity. The calculation of duration, the use of duration, the limitations of duration as a measure of bond price risk, convexity and its relation to the interest rate are key concepts to understand the interest rate risks in fixed income securities.

• The full valuation approach to measuring interest rate risk involves using a pricing model to value individual bonds and can be used to find the price impact of any scenario of interest rate/yield curve changes. Its advantages are its flexibility and precision.
• The duration/convexity approach is based on summary measures of interest rate risk and, while simpler to use for a portfolio of bonds than the full valuation approach, is theoretically correct only for parallel shifts of the yield curve.
• Callable bonds and pre-payable securities will have less interest rate risk (lower duration) at lower yields and putable bonds will have less interest rate risk at higher yields, compared to option-free bonds.
• Option-free bonds have a price-yield relationship that is curved (convex toward the origin) and are, therefore, said to exhibit positive convexity. Bond prices fall less rapidly in response to yield increases than they rise in response to lower yields.

• Callable bonds exhibit negative convexity at low yield levels; bond prices rise less rapidly in response to yield decreases than they fall in response to yield increases.
• Effective duration is calculated as the ratio of the average percentage price change for equal increases and decreases in yield to the change in yield,

Effective Duration = (V V+) / 2Vo(Δy)

• Approximate percentage change in bond price = -duration x change in yield in percent.
• The value of a put increases at higher yields and decreases at lower yields opposite to the value of a call option. Compared to an option-free bond, a putable bond will have less price volatility at higher yields.

• Macaulay duration and modified duration are based on a bonds promised cash flows, while effective duration takes into account the effect of embedded options on a bonds cash flows.
• Modified duration is derived from Macaulay duration and offers a slight improvement over Macaulay duration in that it takes the current YTM into account. Like Macaulay duration, and for the same reasons, modified duration is not an appropriate measure of interest rate sensitivity for bonds with embedded options. For option-free bonds, however, effective duration (based on small changes in YTM) and modified duration will be very similar.
• Effective duration is appropriate for estimating price changes in bonds with embedded options in response to yield changes; Macaulay and modified duration are not.
• The most intuitive interpretation of duration is as the percentage change in a bonds price for a 1% change in yield to maturity.
• The duration of a portfolio of bonds is equal to a weighted average of the individual bond durations, where the weights are the proportions of total portfolio value in each bond position.
• Portfolio duration is limited because it gives the sensitivity of portfolio value only to yield changes that are equal for all bonds in the portfolio, an unlikely scenario for most portfolios.
• Because of convexity, the duration measure is a poor approximation of price sensitivity for yield changes that are not absolutely small. The convexity adjustment accounts for the curvature of the price-yield relationship.

• Incorporating both duration and convexity, we can estimate the percentage change in price in response to a change in yield of (Δy) as:

[-duration x (Δy)J + [convexity x (Δy)^2]> x l00

Effective convexity takes into account changes in cash flows due to embedded options, while modified convexity does not. The difference between modified convexity and effective convexity mirrors the difference between modified duration and effective duration. The price value of a basis point (PVBP) is the dollar change in the price/value of a bond or a portfolio when the yield changes by one basis point, or 0.01 %. We can calculate the PVBP directly for a bond by changing the YTM by one basis point and computing the change in value.

Sivananda is currently Senior Manager (Large Corporate) at Axis Bank, He is an FRM from Global Association of Risk Professionals (GARP), USA, and also a CFA. He has previously worked with State Bank of India and Saint-Gobain.

(No Ratings Yet)

Loading.