A credit default swap (CDS) is a bilateral agreement designed explicitly to shift credit risk between two parties. In a CDS, one party (protection buyer) pays a periodic fee to another party (protection seller) in return for compensation for default (or similar credit event) by a reference entity”. (ISDA, 2010)

Credit Default Swap (CDS) are by far the most popular credit derivative and have proven to be the most successful financial innovation. The structure of CDS is somewhat similar to the insurance policy. The market of CDS has heavily expanded and is traded in Over-The-Counter (OTC) market.

This essay will briefly address the structure and the market of CDS, outlining its common products usage by some large institutions. Following the review of financial structure and pricing of CDS. And finally, this essay will also evaluate the risk management and investment applications of such products.

Literature review

Credit default swaps are credit derivatives which are tradable in the over-the-counter (OTC) market. CDS deliver remarkable value to the worldwide economy. CDS have formed a liquid, vibrant marketplace for trading and or offsetting credit risk, outstripping principal market volume. They have the attributes almost similar to as of insurance. In general terms, during the duration of CDS, one party (generally referred to as the protection buyer) pays a periodic fee or a premium to the other party (usually known as the protection seller), to protect against the financial loss it may incur in case if the reference entity defaults or proclaims bankruptcy or another credit event occurs. If that happens, then, the seller of the protection is obligated to compensate the loss to the buyer of the contract by means of a specified settlement course of action. The buyer of the protection is entitled to protection on a specified notional amount (face value) of the reference entity debt. This view has been supported in the work of Anthropelos (2010). It is to say that the protection buyer is short the underlying credit risk and the protection seller is long the underlying credit risk. (Kolb and Overdahl, 2010)

Figure 1

This Figure is a basic common structure (plain vanilla) of the Credit Default Swap. Which only includes one specific reference entity (it could be either entire corporation, sovereign, or specific obligation of loan/debt instrument, bond etc). However, with regard to CDS, Jiang and Zheng (2009) states that if there are two or more reference entities, it is known as Basket CDS. When any of these reference entity defaults, an add-up basket CDS provides the compensation. A first-to-default CDS compensate only when the first default occurs. In relation to a previously negotiated knock-out-option the responsibility of all the other potential defaults can be excluded. A second-to-default CDS provides compensation only when the second default occurs. Following this, an nth-to-default CDS gives compensation only when the nth default occurs. It is also possible to negotiate a combination of defaults as trigger. (Rudolph et al, 2007). After the relevant default has occurred, a settlement is to take place. The payoffs calculation methods are the same as of a regular CDS. The Swaps then comes to an end and no further payments are to be carried out by either party. Moreover, it is more complicated to value the nth-to-default swap compared to normal regular CDS. According to Hull (2010), It depends on the default correlation between the reference entities in the basket. For example, the higher the default correlation, the lower the CDS spread on a First-to-default swap.

Development of the CDS Market

In 1998 and 1999, the international swaps and derivative association (ISDA) originally created a standard contract credit default swaps (CDS), to be traded in the over-the-counter (OTC) market. Since then, the growth of the CDS market has rapidly increased.

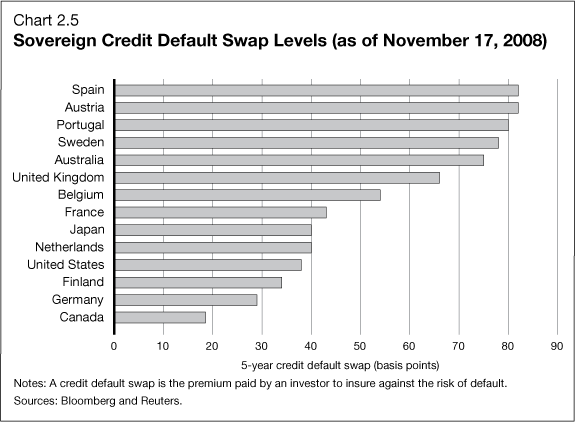
“According to Bank for International Settlements (BIS), in terms of gross market value, the CDS market value increased from USD 133 billion in Dec 2004 to USD 5.7 trillion in Dec 2008 and constitutes the second largest market value after the interest rate contacts”. (European Central Bank, 2009) Other sources says that the outstandings in the credit default market at year 2007 were USD 62.2 trillion, but these number declined to USD 38.6 trillion at December 2008 because of the financial crisis. The outstandings for 2009 are measured USD 30.4 trillion. For the year 2010 a growth is expected again. (ISDA Market Survey, 2009)

The reason was mainly due to the re-pricing of the credit risk and the increase in the volatility in the market during this period. However, in contrast to figure 2, the second half of the year 2008, there was a significant drop in the CDS market size.

Figure 2

In 2007 and 2008, when the credit turmoil had begun, the first major investment bank to fail during the global financial crisis was Bear Stearns (Liuling and Mizrach, 2010). The regulatory concerns were fuelled by the downfall of the insurance giant AIG. The protection proved very costly to AIG also that the company was bailed out by the U.S. government. AIG had been selling CDS protection excessively, without hedging against the odds that the reference entities might decrease in value. This exposed the insurance giant to huge losses.

In the recent publication Hull (2010) states that during this time, trading of many types of credit derivatives were ceased. However, there was almost no impact on CDS, they continued to trade actively. Also, it was at this point in time (Sept. 2008), when Lehman Brothers were having huge number of CDS contracts with them as a reference entity, during this time they declared bankruptcy. “The recovery rate was only about 8 cents on the dollar, so that the payout to the buyers of protection was equal to about 92% of the notional principle. There were some predictions that some sellers of protection would be unable to pay and that further bankruptcies would occur, but on the settlement day (Oct. 2008) everything went smoothly” (Hull, 2010)

Indeed, the CDS market is concentrated around a few large players. In 2008, the five largest CDS dealers were JPMorgan, the Goldman Sachs Group, Morgan Stanley, Deutsche Bank and the Barclays Group (European Central Bank, 2009).

Source: Bloomberg, 2010

The chairman of US security and exchange commission, Christopher Cox (2008) announces that, for CDS trades between financial institutions, Regulatory concerns have led to the development of clearing houses, which restricts financial institutions to post margin on their CDS trades, in the similar way that traders post margin on future contracts.

Baskin et al (2010) state that “International momentum is building for stricter oversight of derivatives trading, as a top U.S. regulator recommended new limits on credit-default swaps and European leaders pushed for a ban on speculative bets against government debt following recent financial turmoil in Greece.” The article also reported that, in a speech by Gary Gansler, Commodity Futures Trading Commission chairman, offered his most precise criticism yet of CDS, often blamed for the collapse of AIG Inc. at the time of financial crisis.

However, ISDA (2010) argues that at the time of financial crisis, financial institutions like AIG, Bear Stearns, Lehman Brothers, took the risk of excessive mortgage loans to borrowers. Their risks were heavily dependent on the way they managed mortgage risk and exposure, as well as their collateral and liquidity management. It also included the failure of AIG financial products and the improper rating of mortgage risk and capital adequacy by the rating agencies. Thus, it means that CDS alone are not to be blamed for the downfall, there are many other sources which are the cause but are clearly neglected.

Pricing and Valuation of CDS

The main idea of a Credit Default Swap (CDS) is to transfer the credit risk of a reference entity from one to another party. In a CDS the party A (protection buyer) pays a periodic insurance premium (“spread”) to the counterparty B (protection seller) until the maturity, or until the reference entity defaults. On the other hand the protection buyer receives a payoff from the protection seller only if the reference entity experiences a credit event. From 2009 if applicable it is to pay an “up-front”. If an index trade is initiated and the quoted price is below the par price then the protection buyer has to make the up-front payment and vice versa. (Kolb and Overdahl, 2010) In the case of a credit event the protection buyer settles the reference asset to the protection seller and therefore the protection seller pays the par value (“physical delivery”). Alternatively, the parties can negotiate “Cash settlement” in which the protection seller has to pay just the par value minus the recovery rate. Additionally, the counterparties can agree to use “Auction settlement”. (Kane and Turnbull, 2003) This method is similar to the cash settlement, unless the recovery rate, so the amount which deducts from the par value, is determined by an auction where potential buyers can make bid on the referenced asset. This method can be very useful in times, where it is difficult to evaluate the asset. (Kolb and Overdahl, 2010)

A credit event is a legally defined event that mainly includes bankruptcy, failure-to-pay, and sometimes debt restructuring events (for European obligators and North American investment-grade entities). (ISDA Credit Event Definitions, 2003)

Usually, there are too many challenging theories and models for the pricing of credit default swaps. There are two most common theories and models for the pricing of the CDS, which are no-arbitrage model and the probability model. However, we will be focusing on the standardised model provided by the ISDA on Bloomberg which is mainly based on the former JP Morgan model.

For the in-depth calculation of the no-arbitrage model. (see Appendix 1) and for the analysis of the probability model (see Appendix 2)

When CDS market first came into existence, the spread of CDS was simply the fraction of the yearly matched maturity default probability. This fraction was determined independently by the forecasted CDS recovery rate.

This simplicity and inaccuracy made the traders questioning the model. And by the time came, different models appeared in the market for pricing of CDS, such as Hull model, JP Morgan model etc. In the year 2009, ISDA announced the transfer of the JP Morgan CDS analytical engine to its company. However, ISDA further made some changes in the model to make it more flexible and now this model is called “ISDA CDS standard model”. Now This model has been set as a standard model and is distributed under free license.

There are two functionality of the of the “ISDA standard CDS pricing” model. First is to convert between spread and upfront and secondly, to compute cash settlement amount. According to Prof. Jarrow, There are two perspectives between CDS spread and default probability, Bottom up approach and top down approach. “Bottoms up approach Builds a model, assume its true, and solve for continuous default probability (“risk neutral”) that matches observable pricing. On the other hand, Top down approach Determines the factors driving the intersection of supply and demand and use an econometric approach to derive (empirical) default probabilities” (van Deventer, 2010).

The ISDA standard CDS converter implies the bottoms up approach and is encoded with the mechanics of settlements. However, this model is too straightforward for accurate valuation and risk management. There are three factors that affect the relation between default probabilities and CDS spread; Interest rate, recovery rate and the constant continuous time default intensity. These three factors are the cause of the simplicity of this model. This view has been supported in the work of van Deventer (2010). ISDA has provided the CDS calculator as an open source, which automatically calculates the pricing of CDS.

Figure 4

For better understanding, let’s take an example of the CDS of Barclays Bank PLC (Figure 4).

The ISDA standard CDS converter is based on simpler assumptions. It assumes the single flat escape rate (hazard rate) instead if the term structure of flat spread. It also assumes that the credit risk starts at the end of the trade date, which is stated 11/17/10 in Figure 4.

It divides the contract coupon days into two types, Riskless days and risky days. Riskless days involve first accrual start day till the trade day. Assuming they have zero chance of credit event. The only fee is contributed through its coupon. Such as in this case, it is from 09/20/10 till 11/17/10, which means 59 days are considered as riskless days.

On the other hand, risky days include the time frame from the trade date 11/17/10 to the maturity 12/20/15. This period is assume to have some probability of default event occurring, which is quantified by the flat hazard rate. In this scenario the payment is made through both, the coupon payment and the and their probability of payment on credit event.

Following the above data, we can say that the riskless accruals coupon days is the converters fee (dirty), and excluding the riskless accrued is the converters points upfront (clean).

In terms of calculation from figure 4, this means:

Buyer pays clean price = upfront * notional

= 0.406855 * 1000mm

= 4068552

Seller pays accrued = <(no. of riskless coupon days)/360> * notional * spread bps

= (59/360) * 1000mm * 0.01

= 1638889

The net amount = 4068552 – 1638889

= 2429663

Risk management and investment applications

Credit Default swaps are very unique and popular, as it offers exceptional value to the economy. In past decades, there has been a sharp rise in CDS activity. Because of their flexibility, its enables the members to better manage their risks, as they can be custom tailored. Over the past few years, CDS appeared to be the primary tool to manage the risks that exist in bank loans and corporate bonds. ISDA (2010) states that, there are several reasons that CDS has strengthen the financial system of the economy, Such as, it enables the banks to shift the risks to the other risk takers. Like this, the banks would be able to make more loans. Also that, CDS provides the significant information on credit conditions of the economy, which can help policy makers and the bankers to manage traditional banking activities. CDS can also help preventing the huge risk concentrations that otherwise would have taken place, and this is because they help distribute the risk broadly throughout the economy.

According to European Central Bank (2009), the most common concern reported in response to the survey was the counterparty risk. There are number of reasons for this measure, such as, Within the financial system, huge concentrated pockets of the counter party risk cannot be measured using aggregate data, because, the availability of the data are not categorized to the level of specific counterparts. Moreover, the data published by the Depository Trust and Clearing Corporation’ (DTCC) and ‘Bank of International settlements’ (BIS) does not match. It would be more effective and efficient if both would have inline data framework. Apart from that, CDS may also have the contribution in the increase of systemic risk.

Figure 3

Looking in the past, financial crises have cleared that, both the buyer and seller of the CDS are exposed to losses, if the counterparty risk materializes. This reflects the possibility for the counterparty to fail to meet its contract payment. “The replacement cost is of the same magnitude for the two counterparties concerned, but with a different sign. For instance, if there is a deterioration in the creditworthiness of the underlying reference entity (i.e. spreads widen), a trade will have a positive value for the protection buyer (i.e. that buyer is “in the money”), as the protection it already has is now worth more. (European Central Bank, 2009)

However, the flexibility and custom-tailoring feature of CDS offers various ways to hedge through its risk, such as, the exposure of this risk can be hedged through offsetting transactions with another party.

Many of the structural characteristics in the CDS market have assisted to change counterparty risk to systemic risk. Shifts from the various institutions, like Lehman Brothers, euro area banking sector and other concentrated in small groups of dealer have impacted the financial system. This would also lead to exposure to market risk, if the CDS spread would increase. If CDS spread were to increase, this would lead to exposure to market risk. The low level of liquidity resulted by the financial crises and with the current high level of market concentration, they both are having huge impacts on increase in the bid ask spread. Recently market is appearing to have more volatility than before, The problem with CDS are that, the effect on one CDS would have the impact on the other CDS in the market.

Conclusion

The CDS swap market is a “young“ market which has grown very fast rapidly in the last past years. Within the last past years the CDS market performed impressively with a huge increase up to approximately USD 60 trillion within a decade. Despite the financial crisis and the market break-in, many market participants argue that the CDS swap market will have a secured future in the financial world because CDS provide a lot of opportunities to participants to hedge risk and to sustain a liquid market. Actually, it is to point out that in the near past CDS service provider like ISDA and Markit take effort for a unique and more transparent market which could be an indication for sustainability of this market.

Our aim in this paper was to give an overview about CDS as a whole. We introduced by giving a definition and explaining the structure and the different innovations in it. Then we showed the market development and performance, as well the interference with the subprime crisis which became a later financial crisis. In relation to this event, we set out reactions of the market participants. Furthermore, we applied the valuation models for CDS swaps. Here, we analysed the two traditional models, the no-arbitrage and the probability model and we supported the theory by providing some calculations in the Appendixes. In this part we also explain the Bloomberg CDS valuation tool. Additionally, we coded our own application, a simple calculation model on Microsoft Excel (see Appendix 1) which is marginally based on Hull’s no-arbitrage model. Last but not least we presented some risks and how these are managed by market participants in practice.

To conclude, we want to mention that the CDS swap market will certainly grow very fast and it will play a. In future, CDS market will certainly further rise and continue to play decisive role in the world of finance. Definitely, some innovations won’t establish. However, derivatives especially CDS could be developed to “financial weapons of mass destruction” if there won’t be an effective regulation and control by authorities, as it entails the heavy feature of custom-tailoring to suits its user needs.

Appendix

Appendix 1

At the moment, when the two parties agree, the CDS spread is defined by the market. The Fair Value (FV) is equal to zero. In a credit event the FV is defined via the par value default payment from the protection seller to the protection buyer. The question is how to evaluate a CDS during the contract period before a credit event happens or not.

A typical CDS contract can usually divided in two potential cash flow streams — the premium leg (or fixed leg) and the protection leg (or contingent leg). It is to take account that the cash flow stream on the premium leg really exists. On the contrary the cash flow on the protection leg is fictitious. However, a physical cash flow could be generated on this side if the protection buyer resells the protection (e.g. in the CDS Market). The value of the CDS contract is at any given time the difference between the present value of the protection leg, which the protection buyer expects to receive, and the premium leg, which the protection buyer expects to pay. (Nomura Fixed Income Research, 2004) So we get

Value of CDS (to the protection buyer) = PV of protection leg – PV of premium leg

The main figures we need to calculate the value of CDS are the default probability/ the survive probability of the referenced entity, the recovery rate and the risk-free discount factors. In general it is to mention that the higher the probability rate and lower the recovery rate the higher the higher the cost for the protection buyer.

First, we will determine the PV of the premium leg. According Hull and White (2000), the adopted formula for PV for the payments of the first part of the premium leg is:

This is the sum of the PV of all spread payments paid by the protection buyer to the protection seller till the default, which is the discount factor for the particular payment date D(ti) multiplied by the survival probability at time t q(ti), multiplied by the annual CDS premium S, multiplied by the accrual days expressed per anno between the payment dates di. The discount factor has the purpose to convert the future payments or payoffs into present value. Additionally, this first part expresses the value of the single spread payment for a single payment period. And these payments must be multiplied by the survival probability because in the case of credit event they are omitted.

The second part of the premium leg includes the value of the accrued premium payments which are paid up to the date of default. We assume that default accurs at the middle of the interval between two payment dates. This means between date ti-1 and payment date ti. This probability is given by . So, the accrued spread amount is the Spread S multiplied by payment date d divided by two Sd/2.

We assume that default accurs at the middle of the interval between two payment dates. This means between date ti-1 and payment date ti. This probability is given by . So, the accrued spread amount is the Spread S multiplied by payment date d divided by two Sd/2. According to the declarative statements above, the PV for the premium leg defined as

For the value of the protection leg, we assume the following: The default will occur at the middle of the interval between two payment dates . And that in case of a default the value of the CDS is given by the unsecured part of the par value. So, the contingent payment is (1-R), where R is the recovery rate. So, the PV of the protection leg is the discounted and summed up expected payment.

To finish it is to say that the value of CDS to the protection buyer must be:

In this case the spread S can be determined as

To make it clear we applied our own excel application tool on Microsoft Excel, base marginal on Hull model.

For the following calculation we assume:

The default probability is the marginal probability on default on the underlying reference that the protection buyer does not need to own. We assume that there is a 0.9% chance each year that the underlying reference will default. We also have an assumption about the recovery rate. This means that in default the recovery will be 35% and the conditional loss 65%. The risk free rate is 5%.

The CDS has a probability of survival in of 99.10% in the first year. In the second year this probability is 98.21% (99.10%*99.10%) and 97.32% (98.21%*99.10%) in the third year and so on. This is a cumulative probability of survival. The probability of survival multiplied by the discount factor gives us the discounted PV of expected payments from the protection buyer to the protection seller (premium leg – part 1). But on this we have to add the accruals because the PV of expected payment covers just the case of non-default. Default happens 6 months into year. The buyer has to pay the seller the accrual portion as the premium payment. And so in this case we are multiplying the 0.90% by 0.5 because there is a 0.90% chance to a default but the buyer is only going to accrual half of that (premium leg – part 2). So similarly here we are present valuing to compute the PV of expected payments if there is a default.

We do this for the protection seller as well. However, we only need to consider the one scenario because if there is no default the seller has not to pay (protection leg). So, the seller just cares about the default.

We are looking for probabilities, and in the first year there is a probability of 0.90% chance of default. In the second year there is a 0.89% marginal probability of default. The probability in the first year is multiplied by the probability in the second year. The percentage of the notional/principal is the default probability multiplied by one minus the recovery rate (0.009*(1-0.35)). We have to discount again because we need the PV terms and we get the discounted percentage of the notional.

Then we assume that the total expected payments are equal to the expected payoffs and we solve for spread S. In this calculation the spread S is 60 basis points of the notional.

Appendix 2

Probability model takes the present value of a series of cash flows, which are weighted by their probability of non default. This model implies that CDS should trade at a significantly lower spread than corporate bonds. From the article of J.P. Morgan (2000), under the probability model, a CDS is priced using a methodology that takes four inputs, (1) the issue premium, (2) the recovery rate, (3) the credit curve for the reference entity, (4) the Libor curve.

In the case, where default event does not occur, then calculation of the price of CDS is simply the sum of the discounted premium payments. On the other hand, taking the possibility of the credit event occurrence, let’s take the example by Kane and Turnbull (2003) for the purpose of explanation.

One year CDS with the effective date ‘t0′. having quarterly premium payments at time t1, t2, t3, t4 respectively. Taking ‘N ‘ as the nominal value and ‘c ‘ as the issue premium. Then the quarterly premium payment size is ‘Nc / 4′. In such case, there are five possible outcomes. One is that, if the contract survives for the time till maturity and rest four are the case of default occurring at first, second, third or fourth payment date.

In order to Price the CDS, we need to allot the probabilities to these five outcomes. After that, we have to work out the present value of the payoff for all the outcomes. Thus, the CDS present value then is basically the payoff of the present value of these five outcomes multiply by with their probabilities.

Figure 3

The tree diagram (figure 3) illustrates, the time at which the contract has either default event or it survives without default event occurrence. In default event case (shown in blue), it ends up with the payment N(1-R), where R stands for recovery rate. On the other hand, where it survives the default event (shown in green), a payment is made ‘Nc / 4′. And the cash flows are shown on the left and right side of the tree diagram, at a point in time with premium payment (Green) and default payment (Blue).And at the termination of contract, a square signifies a solid shade.

(Source: A Short Introduction to Credit Default Swaps by Dr. Michail Anthropelos)

Suppose that company R has issued a corporate bond to Company B which ends in one year from now and its principal is $1,000. The coupon of the bond, paid at the end of the year, is 7%. B wants to protect itself against the case R and cannot fulfil its obligations. It estimates that some credit events are likely to happen and result the default of R. If one of these events occurs before the end of the year, the value of the bond will lose 60% of its value at the maturity. B contacts Company R and asks to buy the protection through a CDS with the following parameters:

The reference asset is the corporate bond issued by R.

The credit events are the ones that result the default of R and hence the 60% decline on the value of the bond.

The default payment is set to be equal to the 60% loss of B in case of default.

Maturity in one year from now.

S faces the problem of the determination of the premium payment that is going to been asked (upfront) in return for this protection. Entering the CDS

The idea of replication pricing is that S can use a certain number of the reference asset and borrow a certain amount of cash in order to perfectly replicate the above obligations.

If x is the amount of cash invested in the risk-free rate (assumed to be 5% p.a.) and y is the

number of the corporate bond obtained, we need to solve the following equations (two linear equations with two unknowns):

The solutions are x = $1,019 and y = -1. This means that the portfolio:

shorting one corporate bond4 and

investing $1,019 at the risk-free rate,

replicates the obligation of the Company S. The cost of the above portfolio is $19 and is the (unique) non-arbitrage premium payment. It should be clear to the reader that any other premium lead to an arbitrage.

Probability model takes the present value of a series of cash flows, which are weighted by their probability of non default. This model implies that CDS should trade at a significantly lower spread than corporate bonds. From the article of J.P. Morgan (2000), under the probability model, a CDS is priced using a methodology that takes four inputs, (1) the issue premium, (2) the recovery rate, (3) the credit curve for the reference entity, (4) the Libor curve.

In the case, where default event does not occur, then calculation of the price of CDS is simply the sum of the discounted premium payments. On the other hand, taking the possibility of the credit event occurrence, let’s take the example by Kane and Turnbull (2003) for the purpose of explanation.

One year CDS with the effective date ‘t0′. having quarterly premium payments at time t1, t2, t3, t4 respectively. Taking ‘N ‘ as the nominal value and ‘c ‘ as the issue premium. Then the quarterly premium payment size is ‘Nc / 4′. In such case, there are five possible outcomes. One is that, if the contract survives for the time till maturity and rest four are the case of default occurring at first, second, third or fourth payment date.

In order to Price the CDS, we need to allot the probabilities to these five outcomes. After that, we have to work out the present value of the payoff for all the outcomes. Thus, the CDS present value then is basically the payoff of the present value of these five outcomes multiply by with their probabilities.

The tree diagram illustrates, the time at which the contract has either default event or it survives without default event occurrence. In default event case (shown in blue), it ends up with the payment N(1-R), where R stands for recovery rate. On the other hand, where it survives the default event (shown in green), a payment is made ‘Nc / 4′. And the cash flows are shown on the left and right side of the tree diagram, at a point in time with premium payment (Green) and default payment (Blue).And at the termination of contract, a square signifies a solid shade.